Dissection and Tesselation
言葉の定義;Dissection : 切断 、裁断。 ここでは多角形を切って平行移動、回転することにより異なった多角形を形成する過程のこと
Tesselation : 隙間の無いように図形で平面を埋め尽くすこと。
Dissection and Tesselationの代表例このページにあるアニメーションのリスト(ハイパーテキストをクリックするとアニメーションがみられます。) |
||
Table of Contents
1. 図形の変形 (Transformation)
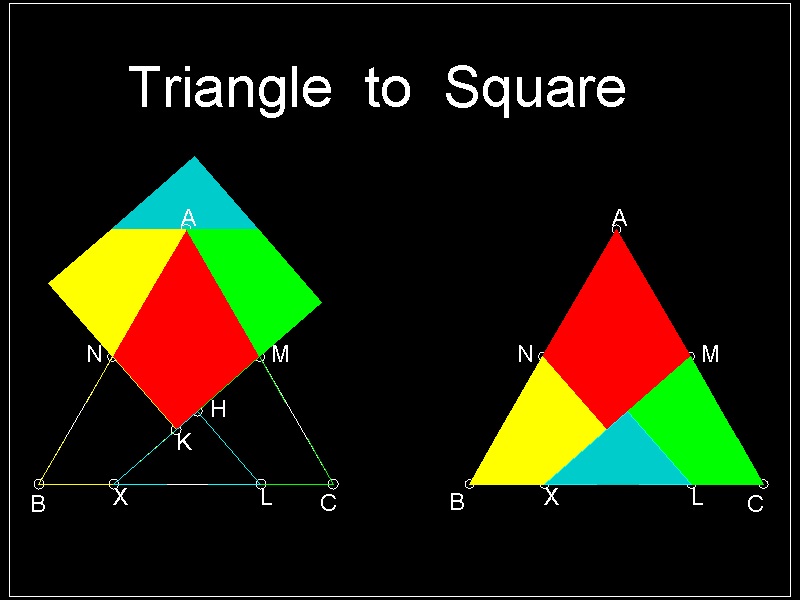
1.1 正三角形から正方形へ
数あるdissectionのなかでも最も単純で美しいのがこの例である。(参考 2, 3, 4, 5, 6).
この図面とアニメーションの作成方法 :
プログラム tr_2_sqr.lsp をロードする。 (load "tr_2_sqr")
コマンドラインから tr_2_sqr と実行命令をタイプする。
このdissection 図中の点 H,K,L,X の見つけ方
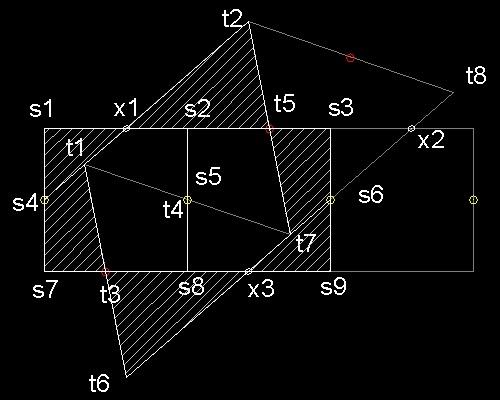
(1) 同じ面積の正三角形 正方形を連ねたもの を水平に並べる。
(2) 正三角形の列を動かして三角形の辺の中点t4 と 正方形の中点s5 が一致するだけでなく 三角形の もう一つの辺の中点t3 が正方形の辺s7 - s8 上 に来るようにする。(左図 参照)点t3 の位置はピタゴラスの定理を使うと 次のように計算できる。
(t3 - s8)2 = (t3 - t4)2 - (s5 - s8)2
この図面とアニメーションの作成方法 :
プログラム tr_2_sqr.lspをロードする。 (load "tr_2_sqr")
コマンドラインから model_analysis と実行命令をタイプする。
最後にハッチングとテキストを追加する必要がある。
****************** tr_2_sqr_model.dwg ******************
ヒンジ付き の場合
文献5は面白いヒンジ付きdissectionについての説明がある。
"正三角形から正方形へ" は この本の最初のdissectionの例である。
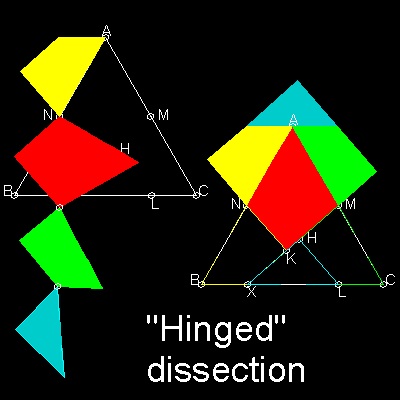
点L,M,N をヒンジで結合すると
図のようにぶらぶらするような形になる。
************* hinged_tr2sqr.dwg *************
1.2 長方形から正方形へ
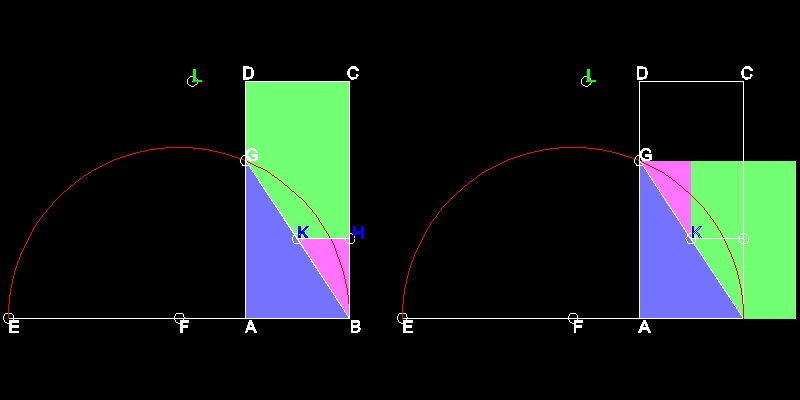
************************************* rec_2_sqr.dwg *************************************
これは AG2 = AB * AEなる関係を利用している。
この図面とアニメーションの作成方法 :
プログラムrec_2_sqr.lspをロードする。 (load "rec_2_sqr")
コマンドラインからrec_2_sqr と実行命令をタイプする。
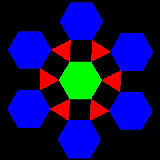
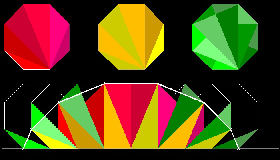
1.3 正方形から八角形へ
これはH.E.Dudeneyによる傑作のひとつである。
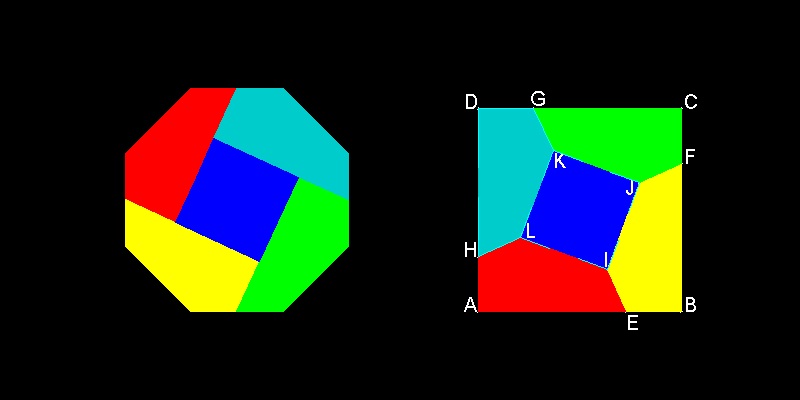
この図面とアニメーションの作成方法 :
プログラムsqr_2_oct.lspをロードする。 (load "sqr_2_oct")
コマンドラインから sqr_2_oct と実行命令をタイプする。
このdissection 図中の点E,F,G,H,I,J,K,L の見つけ方
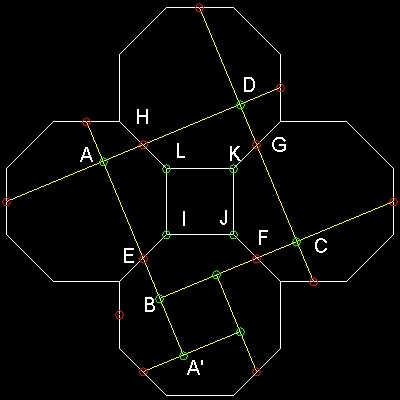
赤い丸で示す点はすべて八角形の辺の中点である。
緑の丸で示す点はこれら赤い点の交差する点である。
************* sqr2oct_model.dwg *************
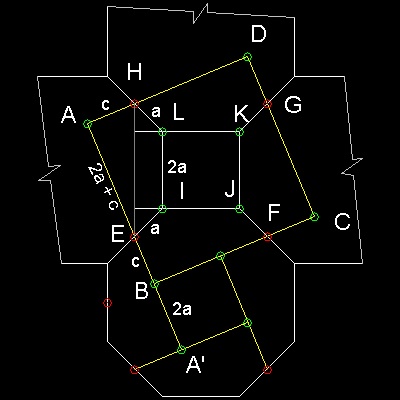
八角形の一辺の長さを2aとする。
すると ∠ HLK = 135 度であるから,
HL = EI = a , HE = 2a + a * √2
AH = c, とすると AE = 2a + cとなる。
AH2 + AE2 = HE2なる関係をつかうと
c の長さが計算できる。
********** sqr2oct_model_detail.dwg **********
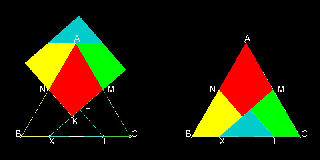
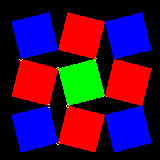
1.4 ギリシャ 十字
ギリシャ十字は5個の正方形からなっていることがわかる。
5 は二個の数字の自乗の和である。 5 = 22 + 12.
ギリシャ 十字 の tesselation は 簡単である。
H.E.Dudeney が 提出した パズル は次のようなものである。
ギリシャ十字を4か5個に切断して、正方形にせよ。
正解の3例を異なる色で示した。
切断線を太い線で示す。 切断された部分を動かすと正方形になる。
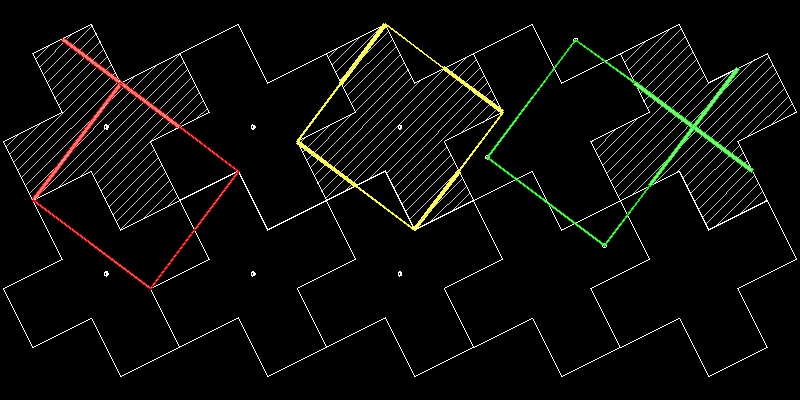
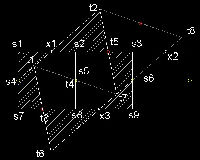
1.5 ヒンジ付き Tesselation
ウェルズ(David Wells) (参考 6) には"ヒンジ付き Tesselation"の面白い例が二つ掲載されている。
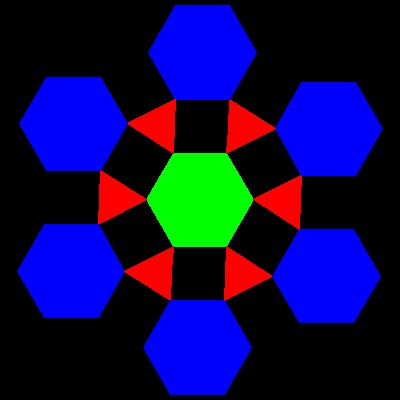
この図面とアニメーションの作成方法 :
プログラムtessel_1.lspをロードする。 (load "tessel_1")
コマンドラインからauto_play
**************** hinge_1.dwg ****************
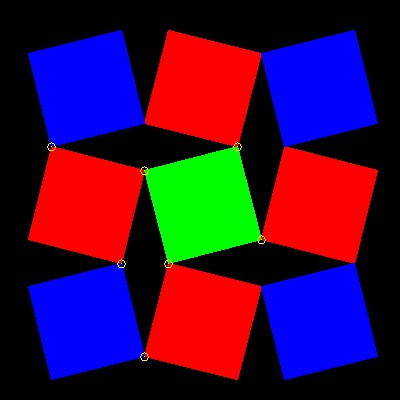
この図面とアニメーションの作成方法 :
プログラムtessel_2.lspをロードする。 (load "tessel_2")
コマンドラインからauto_play と実行命令をタイプする。
**************** hinge_2.dwg ****************
1.6 楕円 から ハート形へ - 3次元 回転
これは3次元回転(ねじり)を利用した非常に単純であるが興味深い変形の例である。(参考 5)
エッサー氏(William Esser III) は回転楕円体の半分を回転させることによりハート形が出来るというアイデア
をアメリカ合衆国の特許として出願し、1985年に認可された。
まずそのアイデアを2次元で説明する。
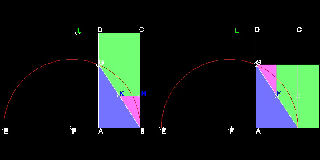
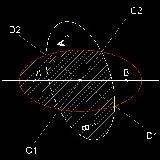
2次元での説明
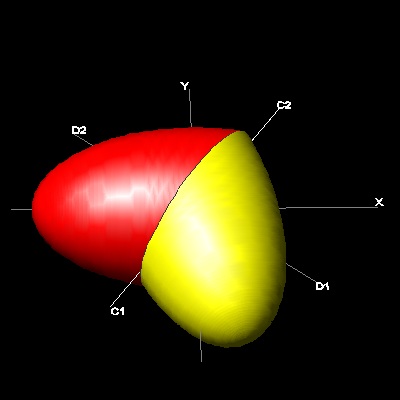
まずその中心を通る直線 C1-C2 によって楕円を二分割する。 A, B はその焦点である。
線分 C1-C2に直角に交わり中心を通る直線をD1-D2 とする。
D1-D2を回転軸として楕円(赤の曲線)を180度回転させる。( 左図でC1 とC2 が入れ替わる)
その結果 として もう一つの楕円(黄色) が得られる。
黄色 と 赤色の楕円を組み合わせると "ハート形" の 領域(斜線)が生まれる。
この図面とアニメーションの作成方法 :
プログラム ellipse_2_heart.lsp をロードする。 (load "ellipse_2_heart")
コマンドラインから ellipse_2_heart_2d と実行命令をタイプする。
*********** ellipse_2_heart_2d.dwg ***********
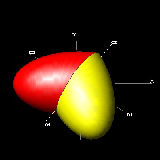
3次元の場合
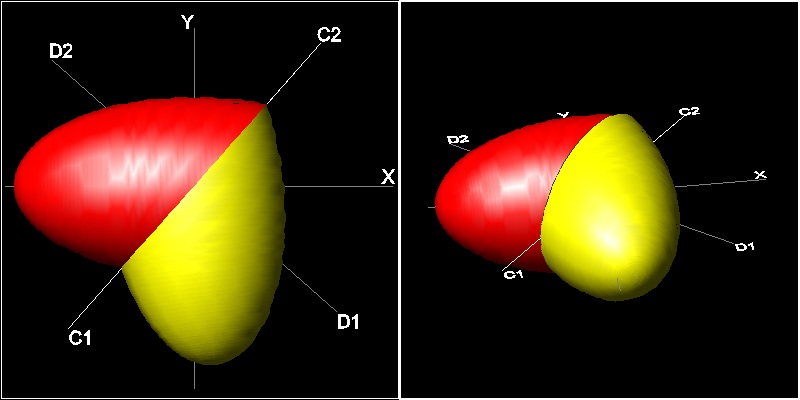
******************************** ellipse_2_heart_2views.dwg ******************************
楕円をその対象軸の回りに360度回転させると楕円体ができる。
その楕円体を2次元の場合と同じように D1-D2 を回転軸に180度回転する。
結果は図に示すような3次元の"ハート形"となる。
この図面とアニメーションの作成方法 :
プログラム ellipse_2_heart.lspをロードする。 (load "ellipse_2_heart")
コマンド ラインから multi_view と実行命令をタイプする。
2. ピタゴラス数 の Tesselation (参考 4)
三個の正方形の辺の長さを x, y , z と する。
4世紀に活躍したギリシャの数学者デオファンタス (Diophantus of Alexandria )
は x2 + y2 = z2
を満たす総ての解を求める 一般的な方法を見つけだした。
その解は約300年後(7世紀)にインドの数学者ブラーマグプタ(Brahmagupta )
によって次のように定式化された。:
すべての解の組み合わせは次の様な形をとる。
x = m2 - n2, y = 2mn , z = m2 + n2
ここで m と n は共通の除数を持たず 、 m + n は奇数である。
(参考 4)によれば解の組み合わせは2つのグループに分かれる。
第一のグループはピタゴラスクラス (Pythagoras class) と呼ばれるもので m = n + 1 である。
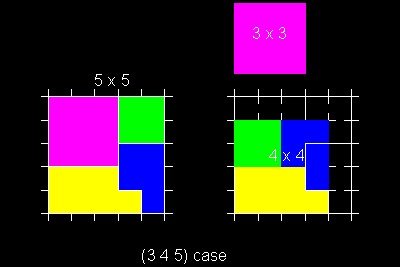
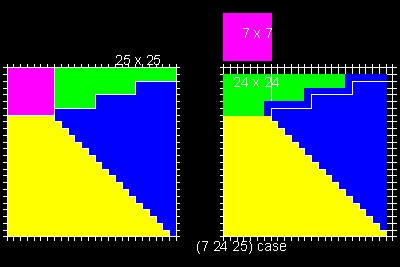
これに属する組み合わせの例は(3 4 5), (5 12 13),(7 24 25),等である。
第二のグループ はプラトンクラス(Plato class) と呼ばれ n = 1 である。
このクラスに属する 組み合わせの例 小さいほうから (3 4 5), (15 8 17), (35 12 37) 等である。
ここでは 第一のグループについて説明する。 第二については将来追加する予定である。
この図面とアニメーションの作成方法 :
プログラム tessel_pclass.lsp をロードする。 (load "tessel_pclass")
コマンドラインからtessel_pclass と実行命令をタイプする。
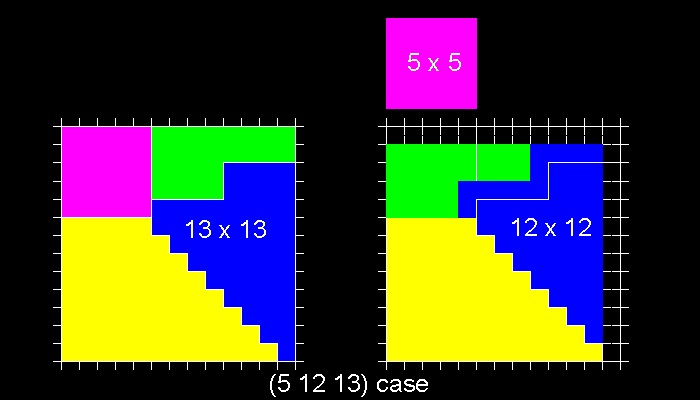
(5 12 13) のケースを見たい場合は, 2を入力する。 (つまり n=2, m=3)
そのほかのケースの結果図
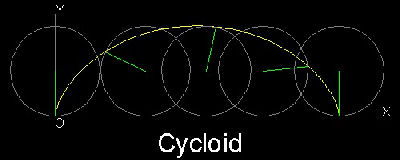
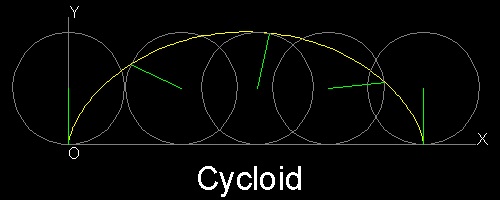
3. サイクロイド に囲まれる面積
(参考 7,11) サイクロイド は 直線の上を転がる円上の点が作る曲線である。その 曲線の式は : x = a(θ - sinθ) , y = a(1 - cosθ)
ここで a は回転円の半径で θ は回転角度 (ラジアン) である。
この図面とアニメーションの作成方法 :
プログラム cycloid1.lsp をロードする。 (load "cycloid1")
コマンドラインからcycloid_curve と実行命令をタイプする。
********************* cycloid_1.dwg *********************
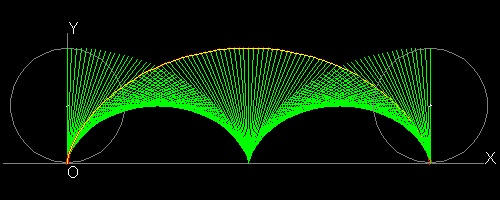
この図面とアニメーションの作成方法 :
上と同じプログラム(cycloid1.lsp)をいじって半径でなく直径を表示するようにすると、面白い曲線ができる。
多くの直線によって2個のサイクロイドが作られる。
これは "Curve Stitching".(参考 12)と呼ばれる ストリングアートの題材の一つである。
********************* cycloid_2.dwg *********************
サイクロイド と X 軸 に囲まれた領域の面積の概算
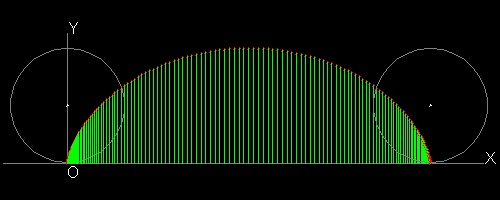
********************* cycloid_3.dwg *********************
この計算をするには コマンド ライン で cycloid_area と入力すればよい。 計算結果はテキスト画面に表示される。
正多角形を利用した可視的証明
この曲線にサイクロイド(Cycloid)と言う名前をつけたのはガリレオ( Galileo Galilei (1564 - 1642) ) である。(参考 10)ガリレオ は1599年にサイクロイドとそれを作る回転円を同じ材料の板から切り出して その重さを比べることにより サイクロイド の面積が円の面積の何倍になるかを見つけようとした。 いかにも 彼らしい手法であると感心せざるを得ない。
その結果 かれはサイクロイドの面積は回転円のおよそ3倍であると解かったが 彼はその比率がもっと複雑な無理数に違いないと思い込んでいたので その実験はそれで終わりにした。
彼の推測が正しかった(ぴったり3倍になる )ことは1634年にRoberval( Roberval (1602 - 1675))によって証明された。
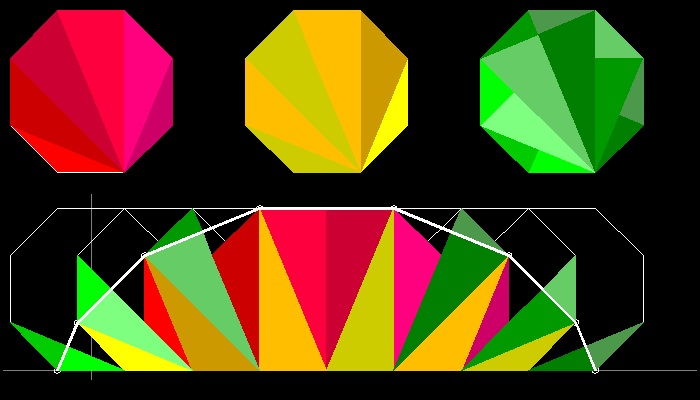
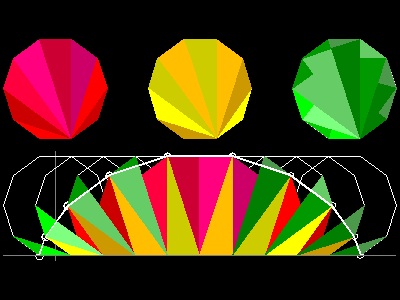
さて円の代わりに正多角形を回転させて その頂点の位置を結んでできる図形と水平軸に囲まれる
面積はどうなるのであろうか。 この場合も正多角形の面積の丁度3倍になることがわかっている。
辺の数を大きくしていけば 円に近ずくので直感的に理解できると思う。
そのことを可視的に示そう。 (参考 7)
この図面とアニメーションの作成方法 :
プログラム cycloid_area.lsp をロードする。 (load "cycloid_area")
コマンドラインから cycloid_area と実行命令をタイプする。
ここに示した正八角形の場合は 8 を入力する。
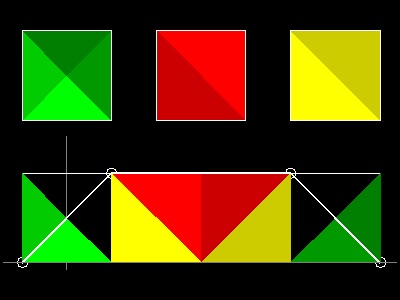
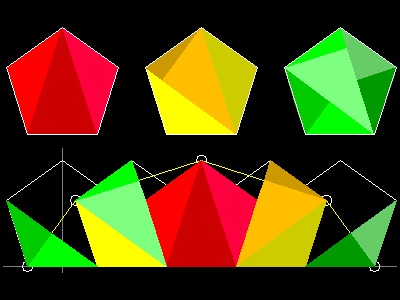
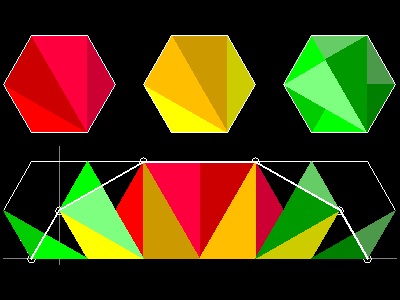
ほかの多角形の場合
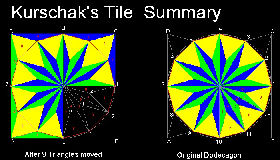
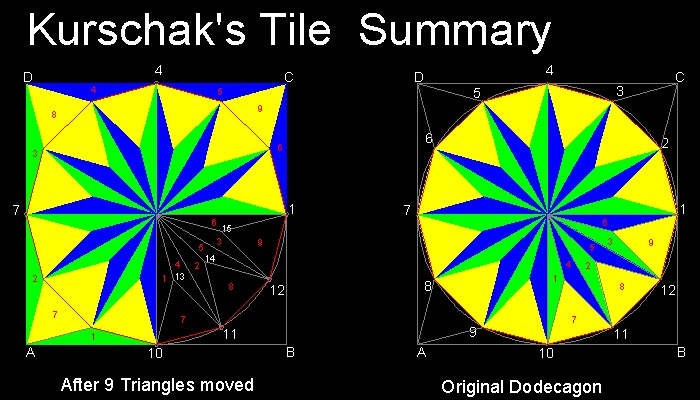
4. Kürschák の タイル (参考 6,7,13)
Kürschák の 定理:
半径が1の円に内接する正12角形の面積は3である。
この図面とアニメーションの作成方法 :
プログラム Kurschak.lsp をロードする。 (load "Kurschak")
コマンドラインからKurschak と実行命令をタイプする。
正12角形の描き方
 1. 正方形を描く。
1. 正方形を描く。
2. 正方形の各辺を底にして内側に正三角形を描く。
3. 三角形の頂点は内側に正方形を作る。
4. 内側の正方形の各辺の中点にしるしを付ける。
5. 左の図に示すように三角形の交点と内側の正方形の辺の中点を結べば
正12角形ができる。
************ draw_dodecagon.dwg ************
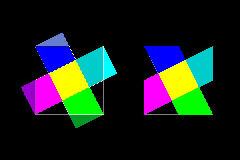
5. 正方形の内部に面積が (1/n)の正方形を作る (参考 7,9)
これは良く知られている Dudeneyのパズルの一つである。
ギリシャ十字を5分割してそれを正方形になるように並べかえなさい。
この分割法は中心の黄色の正方形の面積が外側の正方形の面積の1/5 であることの
証明にもつかわれている。 (参考 7)

************************** sqr_within.dwg **************************
この図面とアニメーションの作成方法 :
プログラム sqr_within.lsp をロードする。 (load "sqr_within")
コマンドラインからsqr_within と実行命令をタイプする。
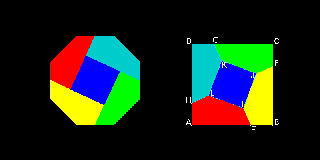
阿部恒氏による折り紙による解と(1/N)の面積への一般化
下の図でABCD は 正方形、E,F,G,Hは各辺の中点である。ABCDが正方形の紙であるとすると線分AE, BF, CG, DH は単純な折り紙の操作によって 折り目として得られる。 これらの折り目の交点が作る正方形の面積が ABCD の 1/5 になるだけでなく たとえば CG と DH の交点の辺CD からの距離が正方形の辺の長さの1/5であることも 折り紙のサークルでは良く知られている。(参考 9)
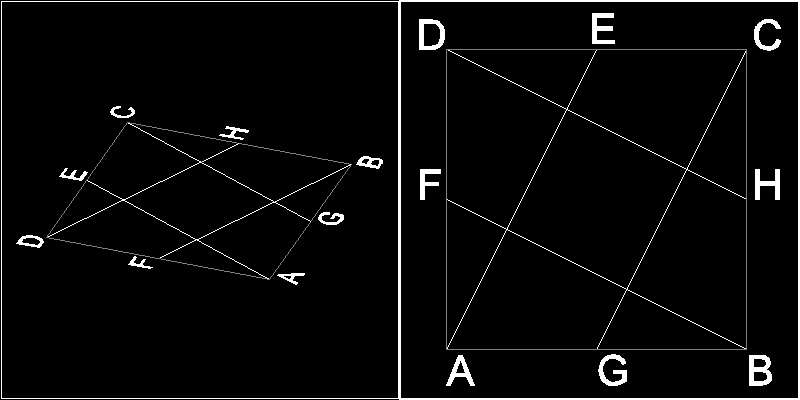
********************************* origami_sqr_within.dwg *********************************
この図面とアニメーションの作成方法 :
プログラム sqr_within.lsp をロードする。 (load "sqr_within")
コマンドラインからorigami_sqr_within と実行命令をタイプする。
阿部恒氏はこの考えを一般化して (1/n) の面積を持つ正方形を作る方法を提案した。
下図を参照しながら説明する。MN はPを通りBC に平行である。
先ず PQRS の面積が(1/5) の場合には 前述のようにMN と BCの距離は辺ABの1/5 である。
つまり MC = NB = (1/5) AB
このことを1/n の場合に拡張すると次のようになる。
(1) MN の折り目をBC から (1/n) の距離につくる。
(2) 頂点A を支点にして頂点 D をMN の折り目上に来るように折ると折り目AEが残る。
(3) 次に頂点B を支点にして頂点 A を AE の折り目上に来るように折ると折り目BFが残る。
以下 頂点C と D についても同様な操作をすると折り目CG ,DHが残る。
その結果 AE,BF,CG,DH の交点が作る正方形の面積がABCD の(1/n) になっている。
以下の右の図に n = 3 の場合の結果をしめす。

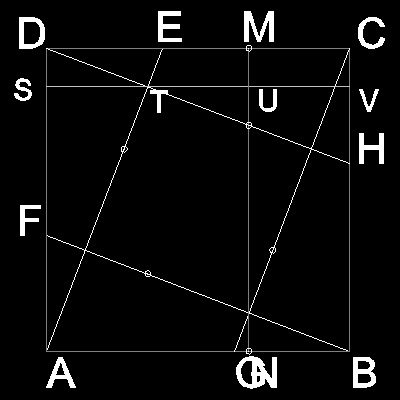
************* sqr_within_fifth.dwg ************
************* one_third_case.dwg ************
この図面とアニメーションの作成方法 :
プログラム sqr_within.lsp をロードする。 (load "sqr_within")
コマンドラインからabe_sqr_within 実行命令をタイプする。
コマンドラインでN の値を3として入力すると1/3の操作が始まる。
(参考 9)による証明を付け加えておく。
上の右の図を参照しながら説明をしよう。 ここで折り紙の辺の長さを1としておく。まず ST = TU = (1/2)(1-UV) であるから
三角形DATの面積 = (1/2)DA x ST = (1/4)(1 - UV) となる。
ところで 内側の正方形の面積 は 全体の面積から この三角形 DAT4個分の面積を差し引いたものであるから
内側の正方形の面積 = ABCD - 4 (DATの面積) = 1x1 - 1x(1 - UV) = 1 x UV
つまり UV の任意の値に対しての(必ずしも1/n の整数比である必要はない。) 内側の正方形の面積が決められることになる。
阿部恒氏の折り紙の手法は次のように言える。
"MN は DA に平行であるとする。 そのとき 内側と外側の正方形の面積の比 は MC/DC に等しい。"
6. Reptiles (参考 8)
1940年にラングフォード( C.D.Langford) は"繰り返しパターンによるタイル" (repetitive tile 略してreptile)についての 論文を発表した。(参考 8)(参考 6) は 最初の形状と全く同じパターンの分割を繰り返し行える形状として 次の11例を列挙している。
それは
- 4 種類の台形
- 4 種類の L 字形
- スフインクス (sphinx) と呼ばれる5角形
- 直角二等辺三角形
- 辺の長さの比が1 対 √2の平行四辺形
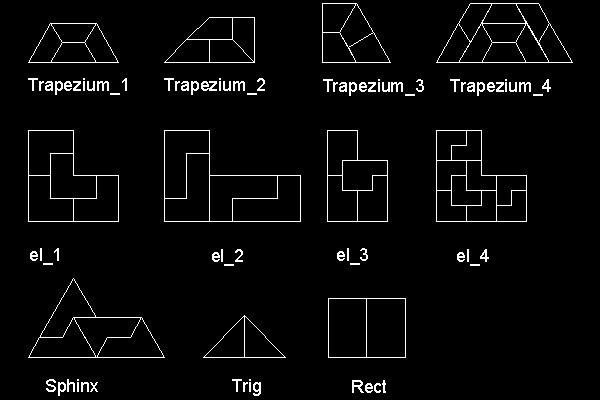
図中で 各形状の下に書かれた名前はプログラムを実行するときのコマンド名である。
ここではスフィンクスを例にとってアニメーションで示すことにする、

この図面とアニメーションの作成方法 :
プログラム reptiles.lsp をロードする。 (load "reptiles")
コマンドラインからsphinx と実行命令をタイプする。
他のパターンについては結果図だけを示す。
ある程度 細かく分割した後、タイルに色をわりあてると、色々変わった模様がえられる。筆者は次のような配色をしてみた。
背景の色を変えてみるのも面白い。
筆者のパターンはあくまでも参考で、読者が色々な組み合わせを試してみることをお勧めする。
分割のレベルによって不思議なパターンが現れて興味深い。
カラー パターンの例
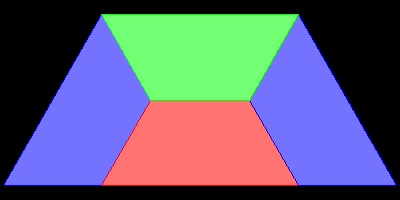
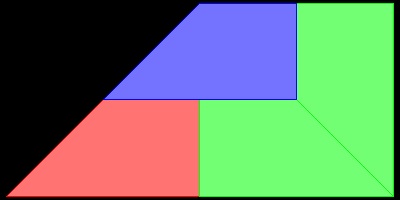
************* shade_trape_1.dwg ************
********* shade_trape_2.dwg ************
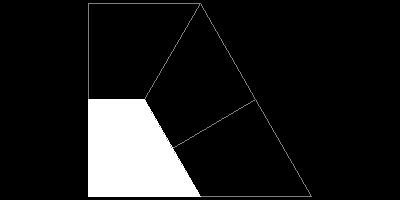
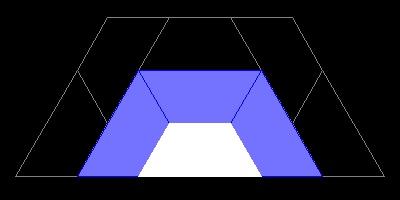
********** shade_trape_3.dwg ************
************ shade_trape_4.dwg ************


************* shade_el_1.dwg ************
************** shade_el_2.dwg ************


************* shade_el_3.dwg ************
*********** shade_el_4.dwg ************
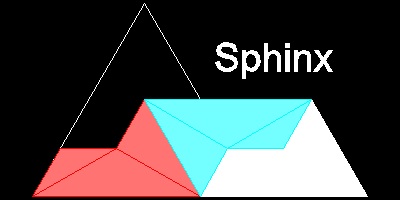
************* shade_sphinx.dwg ************
筆者の配色による結果図









References
- Dudeney,Henry E.: Amusement in Mathematics. Dover, 1958. The original was published in 1917.
- Cundy,H.M.,Rollett,A.P.: Mathematical Models. Oxford Univ. Press, 1961. First edition published in 1951 .
- Lindgren,Harry: Recreational problems in Geometric Dissections & How to solve them. Dover, 1972.
- Frederickson,Greg N.: Dissections: Plane & Fancy. Cambridge Univ. Press, 1997.
- Frederickson,Greg N.: Hinged Dissections: Swinging & Twisting. Cambridge Univ. Press, 2002.
- Wells, David: The Penguin Dictionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, 1991.(Out of print)
- Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA, 2000.
- Langford,C.Dudley: "Use of a geometric puzzle", Mathematical Gazette,No.260,1940.
- 阿部恒 : すごいぞ折り紙 ,日本評論社,2003. ISBN 4-535-78409-4
- Anderson,M.,Katz,.V.,Wilson,R,:Sherlock Holmes in Babylon,MAA,2004
- Haunspenger,D., Kennedy,S. editors: "The Edge of the Universe",MAA, 2006
- Millington,Jon : "Curve Stitching",Tarquin Publications,2001
- Alexanderson,G.L.,Seydel,K. : "Kürschák's tile",Mathematical Gazette,No.421,1978.