************** pi_mc_004.dwg ***************
The problem Buffun proposed (and solved) in 1777 is the following:
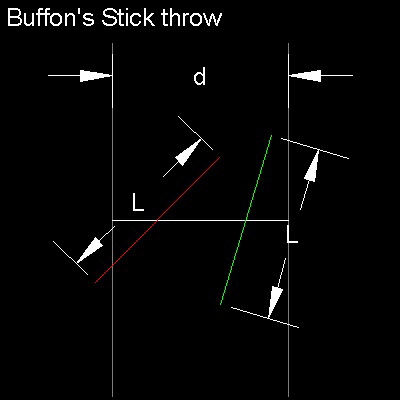
Let a needle of length L be thrown at random onto a horizontal plane ruled with parallel straight lines
spaced by a distance d (greater than L) from each other. What is the probability that the needle will
intersect one of these lines ?

************** pi_mc_004.dwg ***************
Buffon gave the following answer:
Let Nt and Nc be the total number of throw and the number of needles intersecting lines, respectively.
The P, the probability ,defined as the ratio of Nc to Nt (Nc/Nt) = (2 L) / (pi d)
Then, pi = (2L)/(dP)
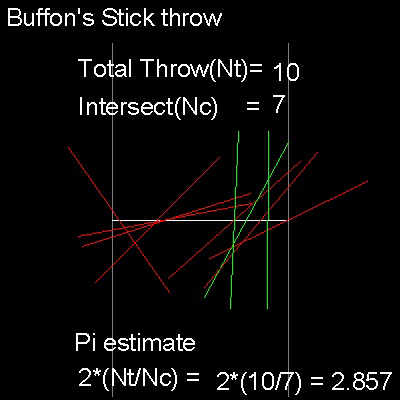
When one makes L = d, pi = 2/P = 2 Nt / Nc . The case of Nt = 10 is shown below.
In this sample trial, Nt = 10, and Nc=7,which gives approximate value of pi as 20/7=2.857
************** pi_mc_004.dwg ***************
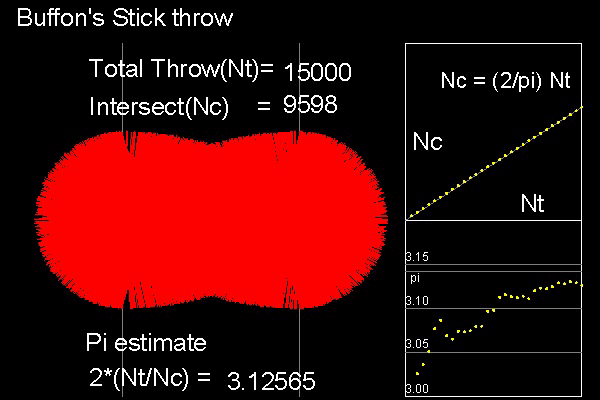
Computer model:
Draw two vertical lines at x = 0, and x=1.
The midpoint of the needle is always on the line y = 0 , between x=0 and 1. And its value is randomly generated.
The value of the angle this needle makes with respect to the x_axis(y=0) is also randomly generated.
Everytime a new needle is created, a test of intersecting will be done, and if the intersection "Yes", Nc will be
incremented by 1.
************************* pi_mc_005.dwg **************************
You can see the process in animation.animation
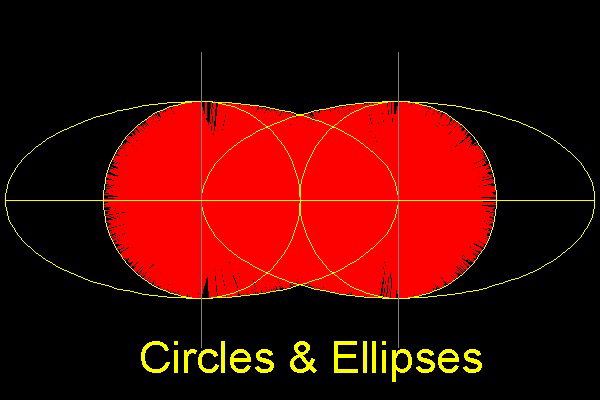
It is interesting to observe that the envelop curves created by sticks crossing the vertical lines are made up of
circles and ellipses.Can you see Why ?
************************* pi_mc_006.dwg **************************
To create this drawing and animation:
Load random_1.lsp (load "random_1")
Load random_2.lsp (load "random_2")
Load Monte_Carlo_pi.lsp (load "Monte_Carlo_pi")
Then from command line, type Buffon