ディノストラトス（
Dinostratus, 約 390 BC - 約 320 BC, は
Menaechmus, 約 380 BC - 約 320 BC,
の兄）は背理法(reductio ad absurdum)を使って次の定理を証明した。
ディノストラトス（
Dinostratus, 約 390 BC - 約 320 BC, は
Menaechmus, 約 380 BC - 約 320 BC,
の兄）は背理法(reductio ad absurdum)を使って次の定理を証明した。
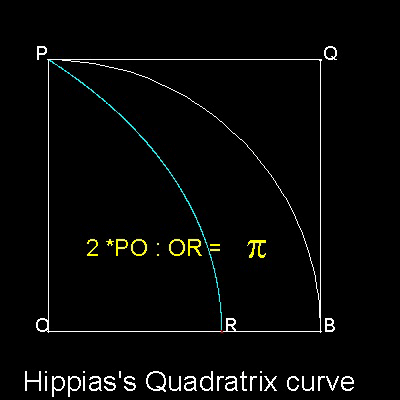
(弧 PB) : PO = PO : OR
または OR = (2/p) PO
この証明の詳細は参考文献１を参照。
この関係の近代的な方法での導き方は次の章で説明。
******* Hippias_circle_squarer_desc.dwg *******
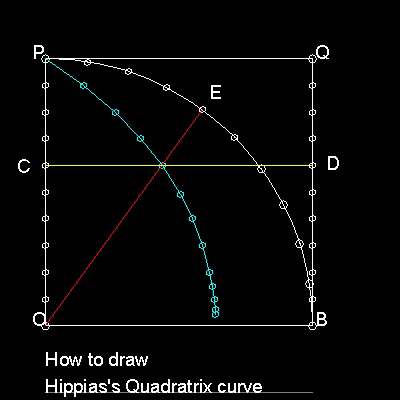OBQP は正方形。
OP と BQ を N等分する。
四分円BP を N等分する。 C, D, E はN等分の点。
水平線分 CD（黄線）と極線 OE(赤線)は交差する。
その交点の軌跡（水色線）が円積曲線である。
*********** quadratrix_curve_10_div.dwg ***********
この図面とアニメーションの作成方法：
プログラム qd_trix.lsp を (load "qd_trix") でロードする。
次にコマンド ラインから quadratrix_2 と実行命令をタイプし、1000分割による円積曲線の図を表示。
テスト図面の実行は test_1 と test_2。
OP と OB を x と y 軸にすると、曲線は y = x tan(p*y/2) で表される。
同一性の tan(a) = sin(a)/cos(a) と、(p/2)y = h で置き換えで
x = (2/p)*cos(h)*(h/sin(h))
ここでh がゼロに近づくと、cos(h) と (h/sin(h)) は 1 になる。
よって、点R の x-座標（円積曲線がX-軸に交差する点）は (2/p) である。
このことから、 p
の値を得るのに長さOR を用い、さらに円の四角化(Squaring the Circle) を行ったことを意味する。
これが、この曲線を円積曲線(Quadratrix)と呼ぶようになった所以である。即ち、円の求積法に関する曲線ということである。
質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。
Last Updated Jan 22, 2007
Copyright 2006 Takaya Iwamoto All rights reserved. .
