ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  ギリシャ時代の円の求積  後世の円の求積

円積問題

スネル(Snell)とホイヘンス(Huygens)

1. スネル(Snell)

スネル( Willebrord van Royen Snell, 1580 - 1626) は反射と屈折の法則の発見者として今日知られている。彼はオランダのLeyden大学でルドルフ( Ludolph van Ceulen, 1540 - 1610)の生徒であった。
ルドルフは、アルキメデスが１９世紀も前に用いた同じ方法を使用し、 pの値を262辺の内接した多角形と外接した多角形を使って小数点３５桁まで計算した。
スネルは、辺数が少ない多角形でp の値を計算できる、より良い上限下限を探し、次の方法を見出した。彼は定理を証明できなかったが（この定理は後にホイヘンス(Christiaan Huygens), 1629 - 1695が証明した）、ルドルフの小数点３５桁をわずか230 辺の多角形で立証した。


************* Snell_Huyg_lb.dwg ************* ************* Snell_Huyg_ub.dwg ************

この図面の作成方法：
   プログラム pi_approximation.lsp を    (load "pi_approximation")　でロードする。
  次に、下限に関しては、コマンド ラインから Snell_Huygens_LB と実行命令をタイプする。 
  上限に関しては、コマンド ラインから Snell_Huygens_UB と実行命令をタイプする。

下限

 
 参考図面： Snell_Huygens_lb.dwg

 BG1 ： 外接する多角形の辺の半分の長さ 
	BG1 = 3r tan b							(1)
 三角形 EOF　の
    　　正弦(sin)定理：	EF/(sin(p-q) = r / sin b			(2)
    　　余弦(cos)定理：	EF2 = EO2 = FO2 - 2EO.FO.cos (p-q)
					=(2r)2 = r2 + 2.2r.r.cos(q)
					=5 r2 + 4r2cos(q)
	よって	EF = r (5 + 4cos(q))1/2				(3)
  (3) を (2)に代入し 
	sin b = sin q / (5 + 4cos(q))1/2				(4)
 等式から  cos b = 1 -sin2 b,
	cos b = (cos q + 2)2 / (5 + 4 cos q)1/2
 そこで tan b = sin q / (2 + cos q)
 従って、
		 BG1 = 3 r sin q /(2 + cos q)

上限

 
  

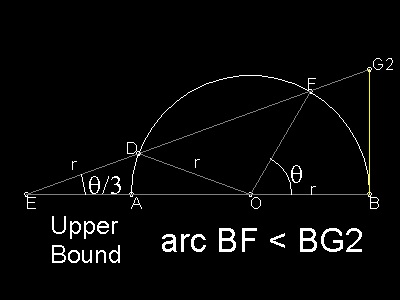
   参考図面： Snell_Huygens_ub.dwg 長さEDをrに等しくする。 ∠DEA = q / 3, これはアルキメデスが
 角 q の三等分に用いた構成と同じである。

 EO = 2r cos(q/3)
 BG2 = EB.tan(q/3) = (EO + r)tan(q/3)
	= r(2 cos(q/3) + 1) tan(q/3)

結果

 
 スネルが発見し後にホイヘンスが厳正に証明したものを次に記す：

	BG1 < 	弧  BF <  BG2
 または
	3 r sin q /(2 + cos q)  <   r q <  r(2 cos(q/3) + 1) tan(q/3)
 
 六角形から始め、多角形の辺数をk倍に倍加(2k 倍)すると、この不等式は次のようになる：
 
	6 x 2k x 3 sin a /(2 + cos a)  <   p <  6 x 2k(2 cos(a/3) + 1) tan(a/3)
 但し、 a = q / 2k = (p/6)/2k
これらの限界の効率を確認するためにサンプルプログラムを実行する。
プログラム "pi_approximation.lsp"　をロードし、Snell_pi と実行命令をタイプする。
結果は次の通り。

** k ** Lower bound         : Upper bound
 error  	 p - LB     :    UB - p  

** 0 ** 3.14023 73433 66169 : 3.14174 00162 53954
 error   	    0.00135531 : 0.000147363

** 1 ** 3.14150 99936 42921 : 3.14160 17882 54884
 error 	  8.26599e-005 : 9.13467e-006

** 2 ** 3.14158 75188 57949 : 3.14159 32233 40417
 error 	  5.13473e-006 : 5.69751e-007

** 3 ** 3.14159 23331 59636 : 3.14159 26891 81042
 error   	   3.2043e-007 : 3.55912e-008

** 4 ** 3.14159 26335 70565 : 3.14159 26558 13962
 error 	  2.00192e-008 : 2.22417e-009

** 5 ** 3.14159 26523 38710 : 3.14159 26537 28799
 error 	  1.25108e-009 : 1.39006e-010

** 6 ** 3.14159 26535 11601 : 3.14159 26535 98480
 error 	  7.81912e-011 : 8.68772e-012

** 7 ** 3.14159 26535 84905 : 3.14159 26535 90335
 error  	   4.8872e-012 : 5.42233e-013

** 8 ** 3.14159 26535 89487 : 3.14159 26535 89826
 error 	  3.05533e-013 : 3.37508e-014

** 9 ** 3.14159 26535 89774 : 3.14159 26535 89794
 error 	  1.86517e-014 : 1.77636e-015  

六角形の結果はアルキメデスの96辺の多角形より良い、また、スネルの96辺の多角形は小数点６桁まで正しい。
彼は更にルドルフ教授のを小数点３５桁まで確認した。

2. ホイヘンス(Huygens)

ホイヘンス(Christiaan Huygens, 1629 - 1695) は「ホイヘンスの原理」という波動原理を発見した物理学者である。
彼はまた数学の発展にも大きく貢献している。
ホイヘンスは２５才にして "De circuli magnitude inventa" という本を出版した。
この本の中で、スネルの見出した二つの限界を厳正に証明している他、円周と面積、内接や外接する多角形の多数の関係を証明している。 
 
  ホイヘンスの結果を幾つかここに紹介する。

参考文献

  ホームページの内容目次に戻る  古代ギリシャ数学の三大問題  ギリシャ時代の円の求積  後世の円の求積

質問、問い合わせは 筆者 岩本 卓也宛てにお願いします。

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved.