Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

Doubling the cube by Greek Mathematicians

Conchoid by Nicomedes

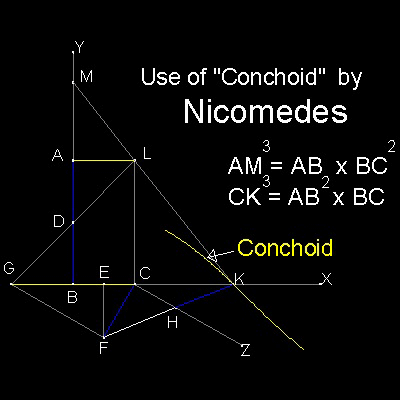
Nicomedes invented a curve named "conchoid" to solve the Delian problem.
It is used to find a point K on X-axis such that line FK passes through
a point "H" on line CZ, and cuts x-axis while HK = CF is being satisfied.

So this process looks similar to "Verging"(neusis) used
by Archimedes, Pappus, and many Greek mathematicians in angle trisection.

Solution using Conchoid

 
 Make rectangle ABCL. D,E are mid-points of AB and BC,

 Extend LD to produce G on x-axis. Erect EF perpendicular to x-axis
 and make CF = AD. Draw CZ parallel to GF.
 Choose a point K on x-axs such that HK = CF.

 Such a point is the intersection of special curve "conchoid" and x-axis.
 This curve can be drawn when F is "pole", CZ is "rule" and CF is "distance".

 Alternative is use a ruler marked with length CF on the edge, and
 find the location of FK (verging,or neusis process)

 Once point K is found, extend line KL to produce point M on y-axis.

 Then AM = {AB.BC2}1/3 and CK = {AB2.BC}1/3

You can see the process using "conchoid" in animation.
******** Nicomedes_Delian_desc.dwg *******

To create this drawing and animation:
   Load Nicomedes_Delian.lsp    (load "Nicomedes_Delian")
  Then from command line, type test_0

Solution using neusis(verging)

Alternative approach is the neusis (verging) technique used by Archimedes,Pappus and other Greek mathematicians in solving angle trisection problem.
A ruler marked with length CF is placed so that one marker is on line CZ and the other, on x-axis while this ruler passes through point F.
So this is an iterative process.

To create this drawing and animation:
   Load Nicomedes_Delian.lsp    (load "Nicomedes_Delian")
  Then from command line, type Nicomedes_Delian

Proof that AM and CK are the solutions

 
 Heath gives the following proof:

 First step is to show MD = FK.
 Since E bisects BC,	BK.KC + CE2 = KF2
 (note:  recall  (a + b) (a - b) = a2 + b2 )
 Add EF2 to both sides;
	BK.KC + CF2 = KF2					(1)
 Since AL is parallel to GK, so is CL to MB,
	MA / AB = ML / LK = BC / CK
 But AB = 2 AD,  and BC = (1/2)GC
 Therefore MA / AD = GC /CK = FH / HK
 and MD / DA = FK / HK 
 Here,DA = HK,therefore MD = FK

 Since D bisects AB, MD2 = BM.MA + DA2
 Combining this with (1) because MD = FK,
	BM.MA + DA2 = BK.KC + CF2
 But DA = CF;  therefore BM.MA = BK.KC
 And 		CK/MA = BM/BK = LC/CK,  
 Whereas, in triangles MAl & MBK, 	BM/BK = MA/AL
 Therefore
		LC/CK = CK/MA = MA/AL
	or	AB/CK = CK/MA = MA/BC

 Then AM = {AB.BC2}1/3 and CK = {AB2.BC}1/3

Go to   Fun_Math Content Table   Three Famous Problems   Delian Problem

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006

Copyright 2006 Takaya Iwamoto   All rights reserved. .