Squaring the Circle

Go to Fun_Math Content Table Three Famous Problems Greek Circle Squarer

Greek Circle Squarers

Archimedes--"On the Measurement of the Circle"

Archimedes (287BC - 212 BC) was the first to give a method of calculating p to any desired degree of accuracy.

His method is based on the fact that the perimeters of the polygons inscribed in a circle and circumscribed about the same circle give lower and upper bound values,respectively, for the circle's circumference.

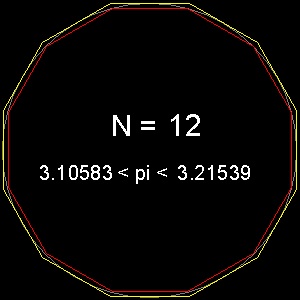
Examples for hexagon and dodecagon are shown below.

********* pi_hexagon.dwg ********* ********** pi_12gon.dwg *********

In these drawings, the diameter is set to 10. So after opening the drawings, look at the values of perimeter.
(Use either "LIST" command or "Properties" option.)
One tenth (1/10) of the perimeter is the approximation for p .

In modern notation

His idea in modern notation is
n(2)^ksin(q/2^k) < p < n (2)^k tan(q/2^k)
where n is the number of sides in polygon, and q is the angle p/n.
k is the number of times "n" is doubled.e.g. k = 2 means number of sides in polygon is n x 4.
Archimedes chose n = 6 for a starting polygon.
So this can be rewritten as
6(2)^ksin((q/6)/2^k) < p < 6 (2)^k tan((q/6)/2^k)

He increased the number of sides for the polygon up to 96(k = 4), and obtained the following result.
3 (10/71) < p < 3 (1/7)
or in decimal,
3.14084 <p < 3.142858
This is an amazing feat considering that computation was done using ratio's(for example square root 3 was replaced by 265/153, etc) and trigonometry was invented 1000 years after his time.

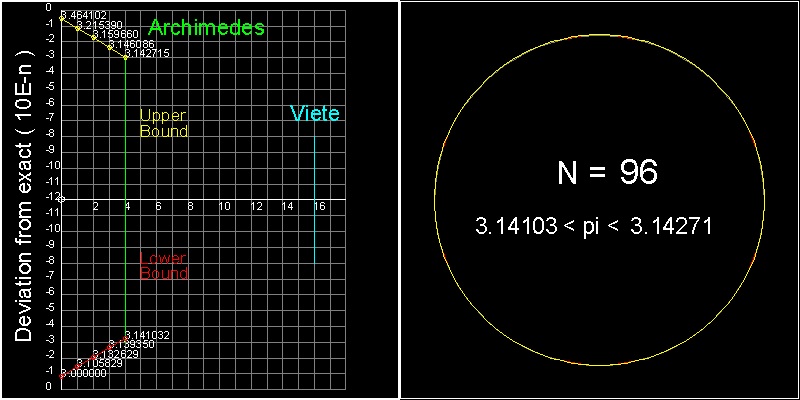
******************************** Archimedes_96_gon.dwg ********************************

You can see the process in animation.

To create this drawing and animation:
Load pi_approximation.lsp (load "pi_approximation")
Then from command line, type Archimedes_pi

Improvement by Viète

Almost 18 centuries after Archimedes,Italian mathematician Leonardo Pisano Fibonacci (1170 - 1250) used the same 96-sided polygon used by Archimedes to improve the accuracy correct to 3 decimal places(3.141). Then a French mathematician Viète (1540 - 1603) revisited the Archimedean concept for pi approximation and by using trigonometry, computed the lower and upper bounds of p for the case k = 16.
That is a polygon of 393,216 sides.( 6 x 2 ¹⁶ = 393,216)
His result was 3.1415926535 < p < 3.1415926537
For reference ,exact value is 3.1415926535897932...

You can see the process in animation.

To create this drawing and animation:
Load pi_approximation.lsp (load "pi_approximation")
Then from command line, type List_pi_number
Then input 17 for repeat cycles.
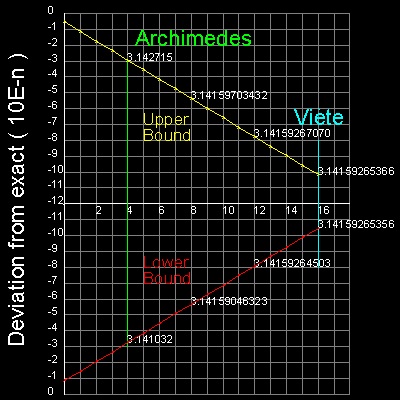
Note: x axis is linear with integer k, and y axis is logarithm with base 10.
For every 4 increment of k, the upper and lower bound values are displayed.

Some readers must have noticed that the lines of upper and lower bounds look straight lines with the same gradient.
That is the right observation and the explanation will be given below.
**************** Viete_pi.dwg ****************

Comments on the slope of the lines

 
 Maclaurin series for sinx and tanx are
	sinx = x - x³/3! + x⁵/5! - ....		(1)
	tanx = x + (1/3)x³ + (2/15)x⁵ +  ....	(2)
Lower bound (LB) and upper bound (UB) are
	LB = 6(2)^k sin((p/6)/2^k) 
	UB = 6(2)^k tan((p/6)/2^k)
Using the first 2 terms in (1) & (2), LB and UB becomes
	LB = p[1 -(1/6)(p/6)²(2)^-2k]
	UB = p[1 +(1/3)(p/6)²(2)^-2k]
Next we define the deviation of LB and UB from the exact value of p as follows:
	F_l = p - LB
	F_u = UB - p
Then
	F_l = (p/6)³ 2^-2k
	F_u = 2(p/6)³ 2^-2k
Taking logarithm of both sides
	log(F_l) = log(p/6)³ - (2log2)k			(3)
	log(F_u) = log{2(p/6)³} - (2log2)k		(4)
(3) ,(4) are the line equation of type y = a + bk
where b is the slope, and a is the y-value when k = 0.

Further Improvement by Roomen and Ludolf

In 1593 Adriaan van Roomen (1561 - 1615) (also known in Latin name "Adrianus Romanus") used 2³⁰(= 1.07374x10⁹) sided polygon to get p value correct to 16-th decimal place. His work is motivated by his communication with Ludolph van Ceulen (1540 - 1610) ,who eventually computed p value correct to 35-th decimal place by using 2⁶²(= 4.61169 x 10¹⁸) sided polygon.

Summary of p value using the idea of inscribed & circumscribed polygons Name No. of sides of Polygon Correct to Archimedes (287BC - 212BC) 96 3.14 Fibonacci (1170 - 1250) 96 3.141 Viète (1540 - 1603) 6 X 2¹⁶ 10-th decimal place Roomen (1561 - 1615) 2³⁰ 16-th decimal place Ludolph (1540 - 1610) 2⁶² 35-th decimal place

References

Heath,Thomas L. :"History of Greek Mathematics Vol. I From Thales to Euclid" Dover 1981

Go to Fun_Math Content Table Three Famous Problems Greek Circle Squarer

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Nov 22, 2006