Dogs at corners of a polygon chasing each other's tail--Equiangular Spiral
List of animations posted on this page.(Click the text to watch animation.)Equiangular Spiral - Zoom View
Equilateral Triangle
Square
Regular Pentagon
Regular Hexagon
Ref.3 describes Equiangular Spiral as follows:
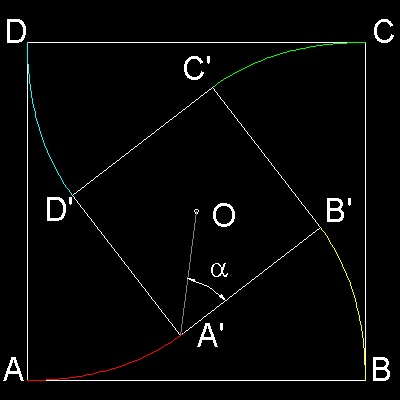
There are 4 dogs ,each of them sitting at the corner of a square courtyard(ABCD) 200 ft x 200 ft.
Each dog is instructed to chase the dog at his right hand side corner.
So the one at A facing towards B,the one at B towards C, and so on , at a
uniform speed of 20 ft. per sec..
Suppose,after some elapsed time, the positions of the dogs that
started at A,B,C and D are A',B',C' and D' respectively.
It is evident from symmetry that A'B'C'D' will be a square and
the direction of the motion of each dog will be at constant angle, i.e. 45º to the
line joining it to the center of the courtyard.(a = 45º)
Since the direction of dog(A) is perpendicular to the direction of dog(B), dog(A)
will catch up 20 ft. every second. So after 10 seconds, the distance between dog(A) and dog(B)
is zero.
************ spiral_model.dwg *************
Before going further, see what the path of the 4 dogs looks like.
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type ndogs
,then input number of sides in polygon : 4
Specify dog's stride as % of side length AB:(def=1%) hit return for default
Specify display speed (1-100) 1:veryfast 100:very slow (def = 50) hit return for default
total_path =1.41421
Such a curve,in which the tangent at any point makes a constant angle with the radius drawn to that point from a fixed point is called an Equiangular ( or Logarithmic) Spiral.
This curve was discovered in 1638 by
Rene Descartes (1596-1650)
during his study of dynamics.
The extensive studies of its properties of self-reproduction were done by
James(Jakob) Bernoulli(1654 - 1705).
He was so much impressed by its properties that he requested the curve to be engraved
upon his tomb with the phrase "Eadem mutata resurgo" ("I shall arise the same, though changed").
Properties and formulas for equiangular spiral
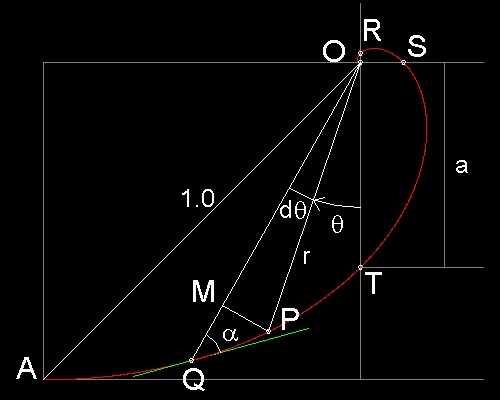In the drawing, cot a = MQ/MP
,where MQ = dr , MP = r dq
So cot a = dr/rdq or cot a dq = dr/r
Integrating with repsect to q,
loger = q cot a + loger0
where r0 is the value of r when q = 0.
This may be written as loge(r/r0) = q cot a
or r = r0 e q cot a
where angle q is counted clockwise.
************ equiangular_spiral_def.dwg *************
In this example, the only known radius which can be used as a reference is the radius OA (= 1.0).
So letting r0= OA, and taking angle q starting from line OA counter clock-wise, equation can be written simply as r = e-q , because cot a = 1
(1) All the radii are cut by the curve at a constant angle (a)
(2) Arc length is the radius multiplied by constant, S = R/cos a
arc length ds = (r2 + (dr/dq)2)(1/2)dq = (1 + r2(dq/dr)2)(1/2) dr
= (1 + (tan a)2)(1/2)dr = (1/cos a)dr
Hence arc length from r = 0 (the center of the spiral) to radius R = R/cos a.
In this square case, the toal arc length = OA/cos a.= 1.0/cos(45) = sqrt(2) = 1.41421356...
(3) Lengths of radii at equal angles to each other form a geometric progression.
Further studies on the Equiangular Spiral curve
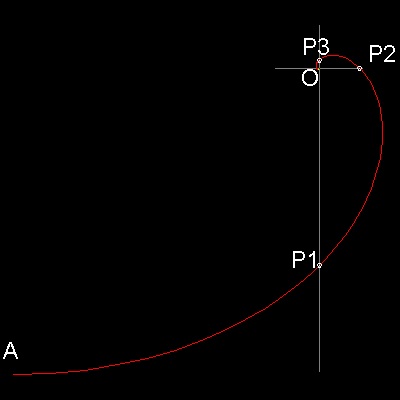This drawing shows how the curve r = e-q looks like.
The curve cuts x & y axis at P1,P2,P3,...and if the distance from the origin O is measured in the
drawing,
OP1 = 0.455488, OP2 = 0.094687, OP3 = 0.019683
Then OP1/OP2 = OP2/OP3 = 4.8105 = ep/2
It means that OP3P2 and OP2P1 are similar,i.e. when OP3P2 is rotated 90 degrees clockwise, and
scaled up by the amount of ep/2, then these two curve
segments are identical.You can verify this by displaying this drawing and zooming up,copying a portion of the curve,and rotating 90. degrees, then scaling up by 4.8105.
*********** equiang_spiral.dwg ************
This is the (3) property stated above. The other porperties can also be verified using this drawing. It is worth a trial.
The whole spiral can be seen by running the Equiangular Spiral - Zoom View .
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type draw_equiangular_spiral
-------------------------------------------------------------------------------------
3 dogs case
You can see the process in animation.
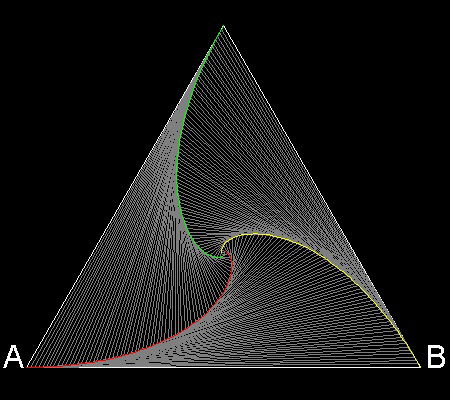
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type ndogs
,then input number of sides in polygon : 3
Angle a = p/6
******************** 3dogs.dwg ********************
4 dogs case
You can see the process in animation.
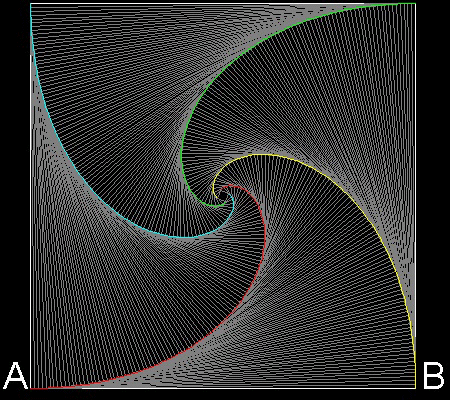
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type ndogs
,then input number of sides in polygon : 4
Angle a = p/4
******************** 4dogs.dwg ********************
5 dogs case
You can see the process in animation.
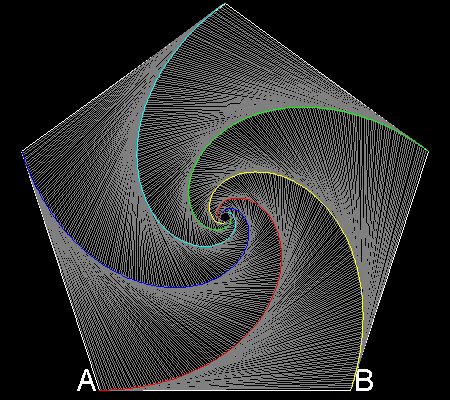
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type ndogs
,then input number of sides in polygon : 5
Angle a = 3p/10
******************** 5dogs.dwg ********************
6 dogs case
You can see the process in animation.
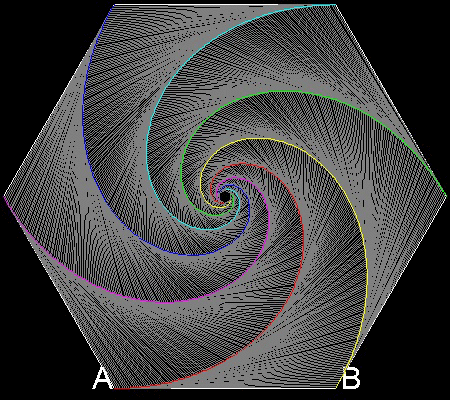
To create this drawing and animation:
Load brocard.lsp (load "brocard")
from command line, type ndogs
,then input number of sides in polygon : 6
Angle a = p/3
******************** 6dogs.dwg ********************