Many Proofs of Pythagorean Theorem
List of animations posted on this page.(Click the text to watch animation.)Use browser's "Back" button to come back to this page.
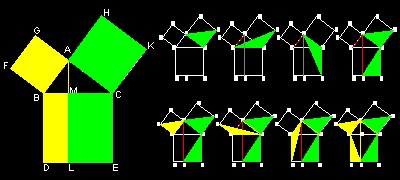
See Euclid's classical solution in animation
Go to Proof by Euclid in "Element"
See Rectangle variation by Lecchio (1753) in animation
Go to Variation of Euclid's proof #1
See Yanney's proof (1903) in animation
Go to Variation of Euclid's proof #2
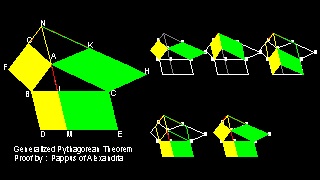
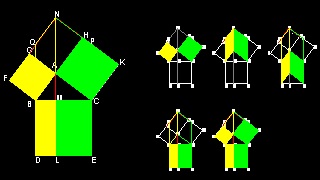
See Generalization to parallelogram by Pappus of Alexandria in animation
Go to Generalization by Pappus of Alexandria
See Graphical proof by Pythagoras in animation
Go to Proof by Pythagoras
See Perigal's dissection (1873) in animation
Go to Corner of smaller square-b is chosen-1 (Perigal)
See variation of Perigals' dissection proof in animation
Go to Variation of Perigal's dissection
See Dudeney's construction of 1917 in animation
Go to Center of larger square-a is chosen (Henry Dudeney)
See Hisashi Abe's origami solution-1 in animation
Go to Origami Solution by Hisashi Abe
See Hisashi Abe's origami solution-2 in animation
Go to Origami Solution by Hisashi Abe
See Mario Pacek's dynamic solution in animation
Go to Dynamic proof by Mario Pacek
See Leonardo Da Vinci's proof in animation
Go to Proof by Leornardo Da Vinci
See Thâbit ibn Quarra's proof in animation
Go to Proof by Thâbit ibn Quarra
See Liu Hui's dissection in animation
Go to Proof by Liu Hui using Dissection
See J.E.Böttcher's proof in animation
Go to Proof by J.E.Böttcher using Dissection
See Generalization to parallelogram in animation
Go to Generalized Pythagorean Theorem for a Parallelogram
Table of Contents
- Proof by Euclid in "Element"
- Variation of Euclid's proof #1
- Variation of Euclid's proof #2
- Generalization by Pappus of Alexandria
- Proof by Pythagoras
- General Concept of Dissection
- Proof by Leornardo Da Vinci
- Proof by Thâbit ibn Quarra
- Proof by Liu Hui using Dissection
- Proof by J.E.Böttcher using Dissection
- Generalized Pythagorean Theorem for a Parallelogram
- De Gua's Theorem: Generalization of the Pythagorean theorem to three dimensions
- Spherical Pythagorean Theorem
Probably the most famous theorem of all Geometry studies is the "Pythagorean Theorem". The name came from the famous
Greek mathematician
Pythagoras of Samos(circa 569-475 BC)
who was a spiritual leader of the group studying mathematics.
In Book I of Euclid's Element, this theorem is stated as Proposition 47.
"In right angled triangles the square on the side subtending the right angle
is equal to the squares on the sides containing the right angle."
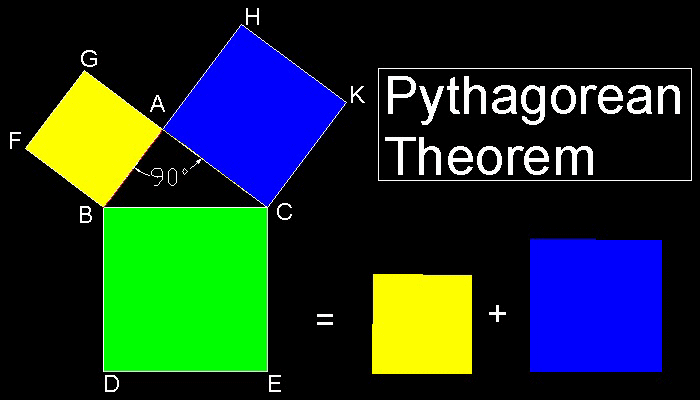
There are far more proofs offered of Pythagoras' theorem than of any other proposition in mathematics. "The Pythagorean Proposition" published by Elisha Scott Loomis in 1940 contains 367 proofs !.
Proof by Euclid in "Element"
You can see the process in animation.
This is one of the most elegant of many proofs. The center of the argumnet is that the areas of triangles ACK, BCK , ACE and MCE are exactly the same. Therefore the areas of ACKH and MCEL ,which are twice that of triangle ACK & MCE respectively, are the same. Similar argument is true for yellow colored parts, i.e.,ABFG & BMLD.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_1
Following two proofs use rectangle and square instead of triangle.
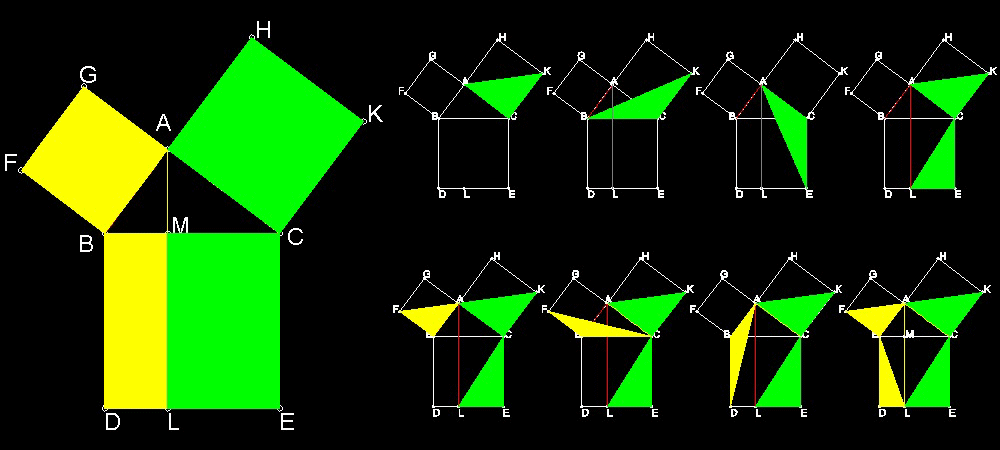
Variation of Euclid's Proof #1
Ref. 1 (Elisha Scott Loomis) lists this proof as Geometric Proof #42, published by Lecchio in 1753.
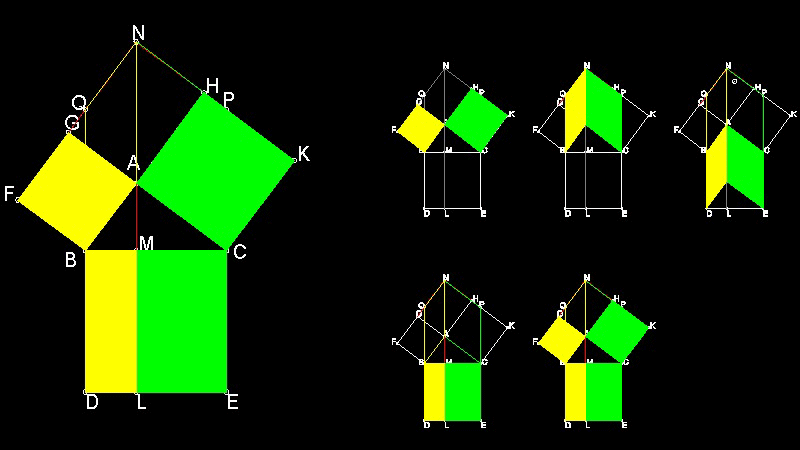
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_3
Variation of Euclid's Proof #2
B.F.Yanney published this proof in 1903 (Ref. 6) (p.283).
This is very similar to #8 .
Areas of LMOA = LKCA = ACED and similarly, areas of HBOM = HBCK = HFDK
Hence ABHL = LMOA + HBOM = ACDE + HFDK
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_9
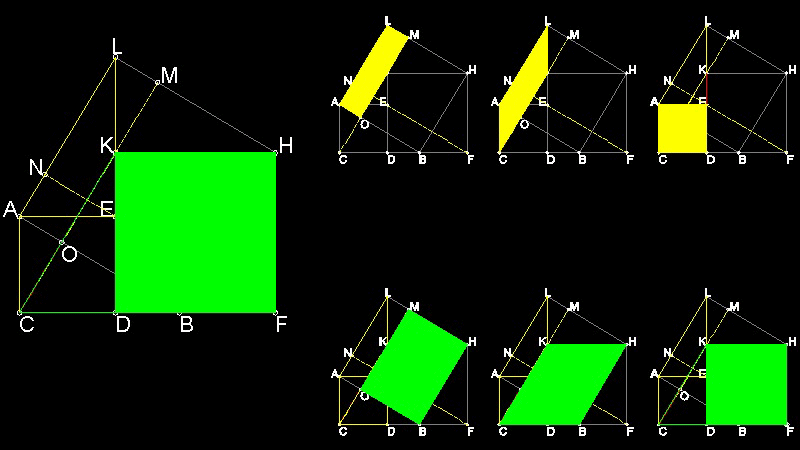
Generalization by Pappus of Alexandria (Ref. 3)
In the figure NA = LM
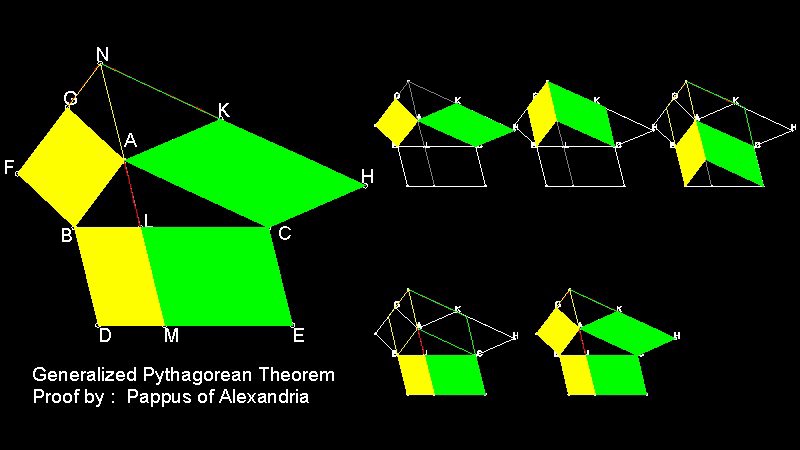
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_4
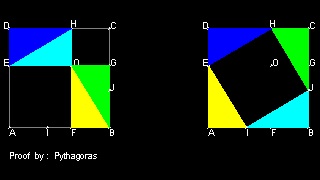
Pythagoras also offered a very simple proof.
Proof by Pythagoras
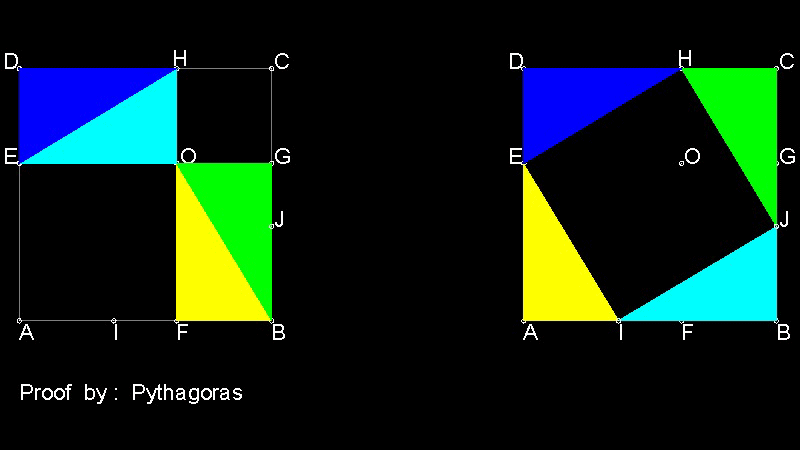
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_7
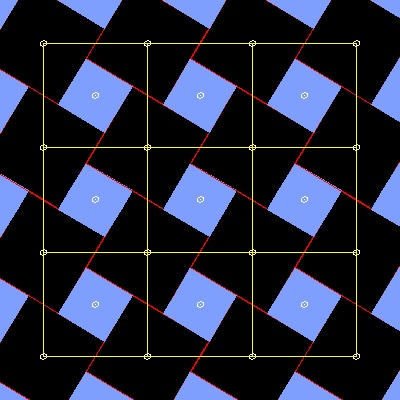
General Concept of Dissection
There are many clever proofs using dissections. The general concept for using dissection can be explained as follows:
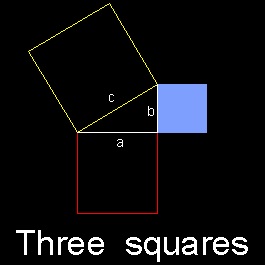

****** tesselation_1.dwg ******
****** tesselation_2.dwg ******
****** tesselation_3.dwg ******
(1)In this example, the size of three squares a,b & c are given.(tesselation_1.dwg)
(2)Create a gapless pattern made up of two squares (a & b).(tesselation_2.dwg)
(3)Create a mesh like pattern using "c" on some transparent paper.(tesselation_3.dwg)
Then move the "mesh-C" over the pattern a-b so that the corner
of mesh-C matches some characteristic points like center or edge of squares.
example follows:

To create this drawing :
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type dissection
Any combination of triangles and quadrilaterals cut out by the yellow square will make up two small squares. So this method will create infinite number of dissection. There are two interesting cases,i.e. center of squares and edge of squares.
Corner of smaller square-b is chosen

To create this drawing :
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type dissection
Then match the corner point to the corner of smaller square.
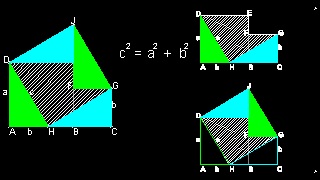
This is Perigal's dissection of 1873.
*********** dissection_case_2.dwg ***********
Perigal's dissection of 1873
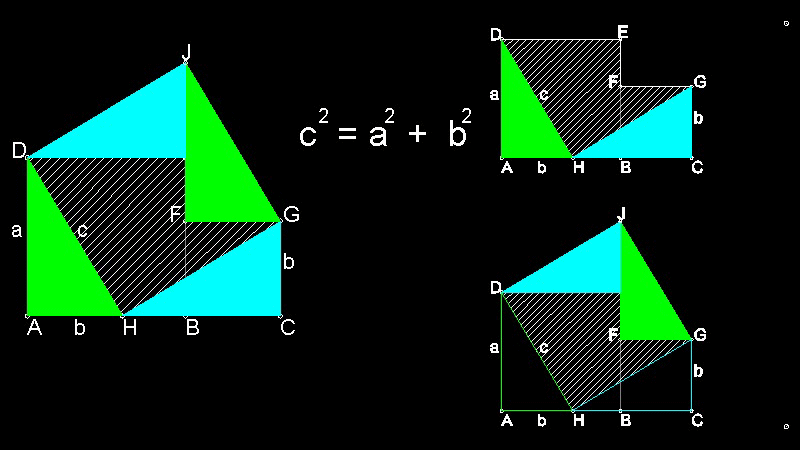
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_2b
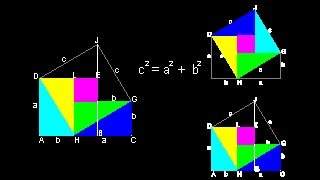
The cross-hatched area in Perigal's dissection can be further divided into one square and 2 triangles. This leads us to the next variation.
Variation of Perigal's dissection
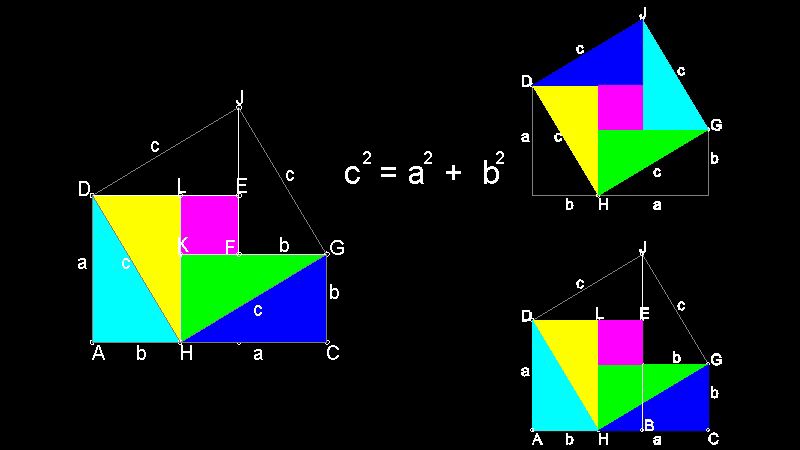
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_2c
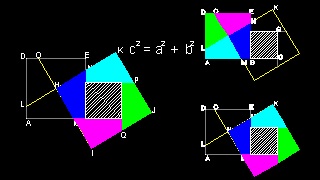
Center of larger square-a is chosen
To create this drawing :
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type dissection
Then select the center of the larger square(b x b).
This is Henry Dudeney's construction of 1917.
************ dissection_case_3.dwg ************
Henry Dudeney's construction of 1917
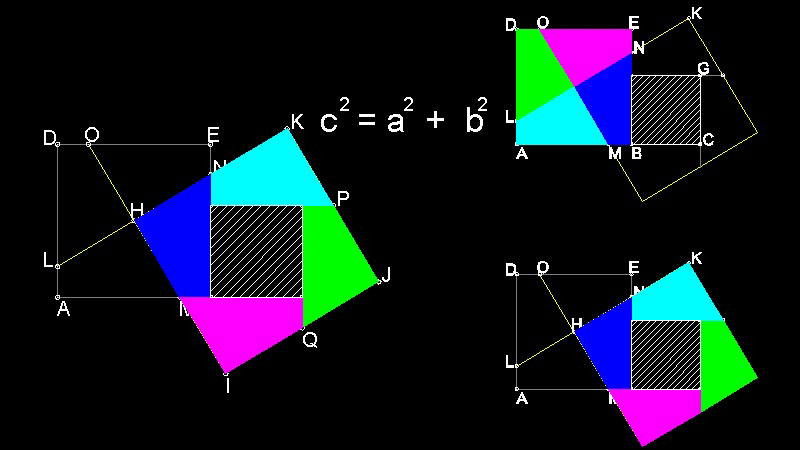
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_2d
Corner of smaller square-b is chosen-2
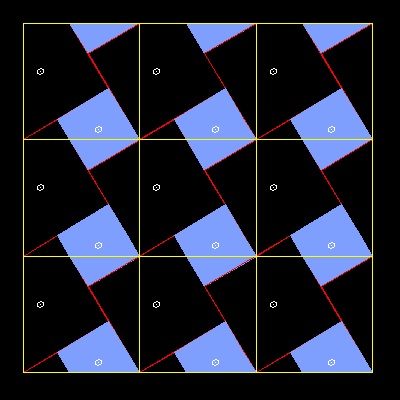
When #5-a case is turned upside down,
and move the yellow frame to a different corner
point of smaller square,
then another interesting dissection is found.
This leads us to the Hisashi Abe's dissection
based on the origami concept.
*********** origami_dissection.dwg ***********
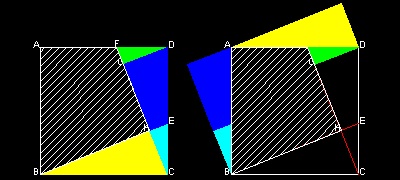
Origami solution by Hisashi Abe
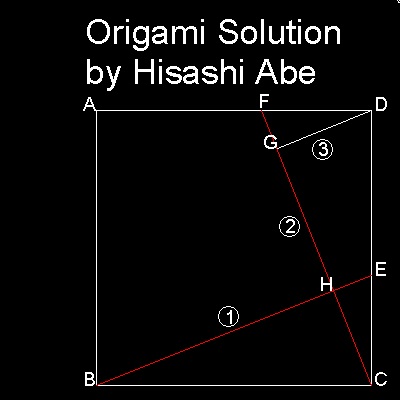
Origami process:Prepare a square piece of paper.
1. fold along line BE.
2. fold line CF by locating point E on line BE.
This makes CF perpendicular to BE.
3. fold line GD by locating F on line CF.
GD is now perpendicular to CF.
Note here that BCH and CDG are identical,
and GD = CH.
Here, this process is done by computer.
To create this drawing :
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Abe_origami
************* Abe_origami_0.dwg *************
Cut out two trianlges BCH and DGC. Move BCH upward so that line BC matches line AD. Move DGC left so that line DC matches line AB.
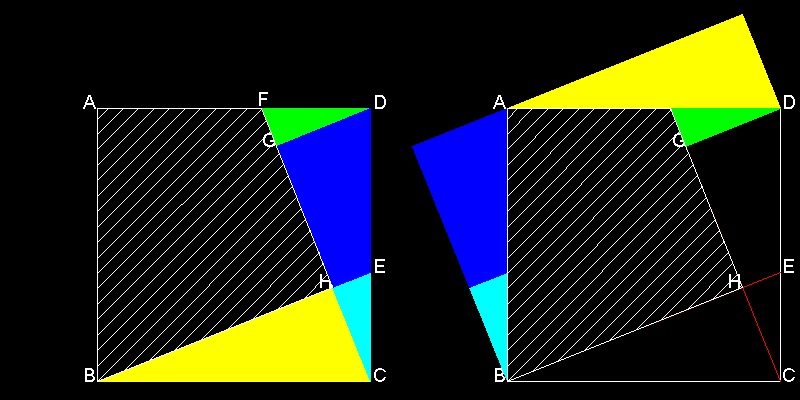
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Abe_origami_a
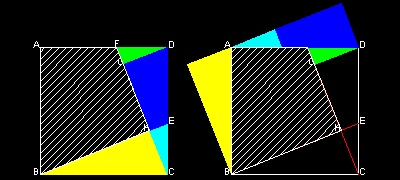
Since BCH = CDG, essentially the same result can be achieved by rotating these trianlges. i.e. rotating BCH around point B, and CDG around point D.
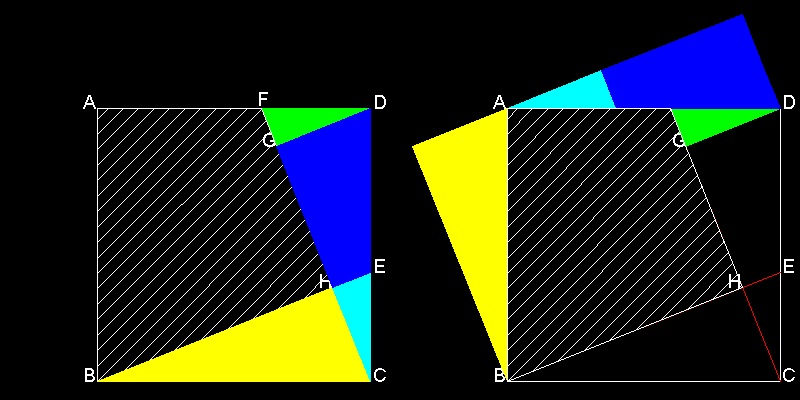
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Abe_origami_b
But this picture does not look neat. The reason is the gap between two small triangles,green and cyan. The picture would look nice and clean if cyan colored triangle and green colored triangle meet at point F. The following solution by Mario Pacek does just that.
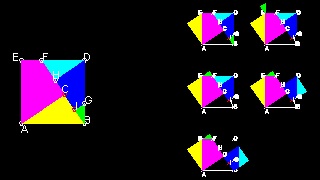
Dynamic proof by Mario Pacek
I found this interesting proof in Pythagorean Theorem by Alexander Bogomolny.Dr.Bogomolny says that this proof was done by Mario Pacek (aka Pakoslaw Gwizdalski).
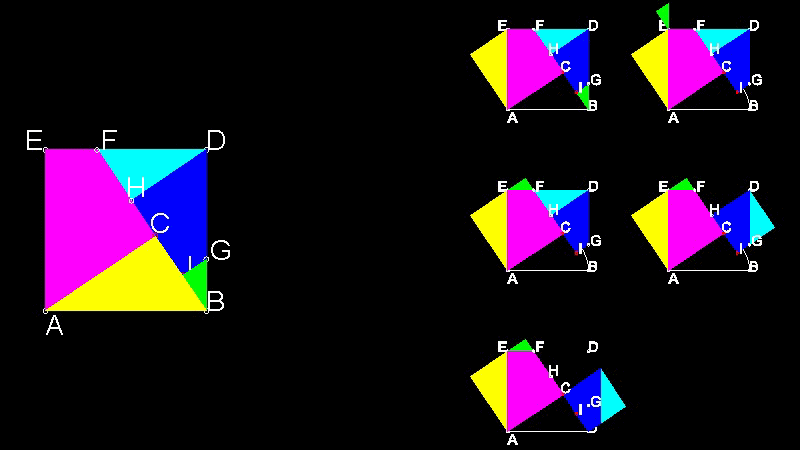
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_8
More of innovative proofs
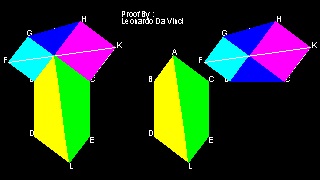
Proof by Leonardo Da Vinci
This is a very famous proof by Leonardo Da Vinci(1452-1519).(Ref.3)(p. 31)
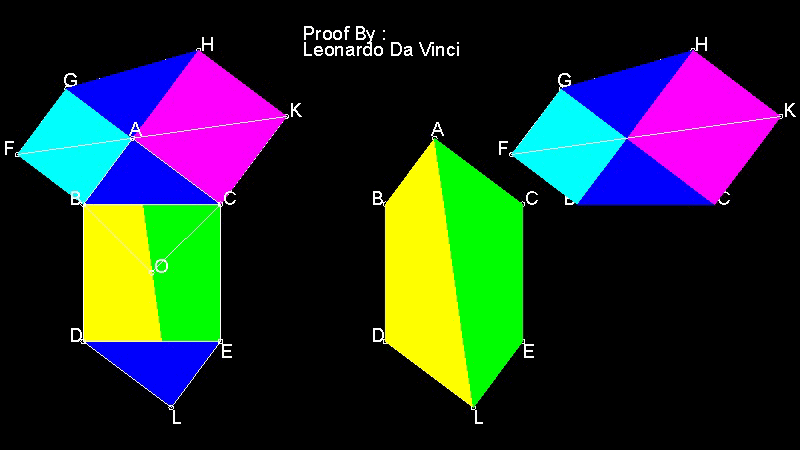
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_5
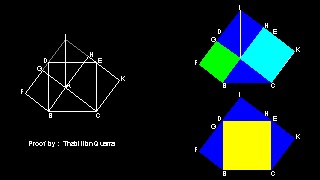
Proof by Thâbit ibn Quarra(828-901)
This proof is by Thâbit ibn Qurra(828-901)(Ref.6)(p 282-283). Ref.6 gives a detailed discussion of his works.
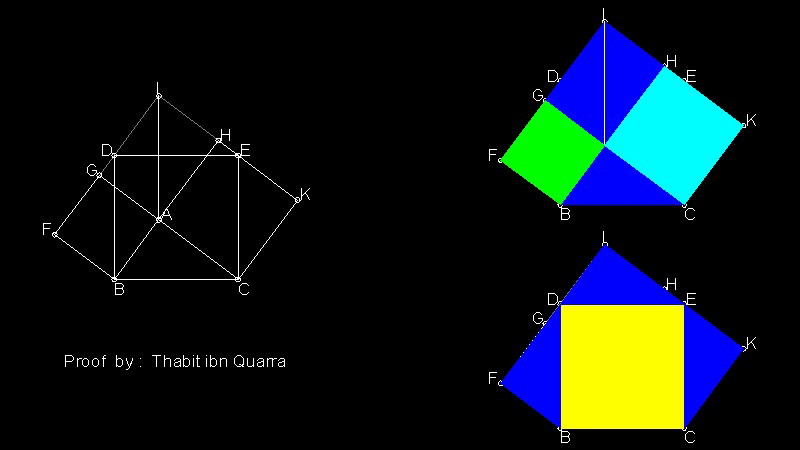
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type Euclid_47_6
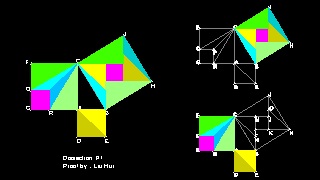
Proof by Liu Hui(3rd century AD) using Dissection
His proof was only in description ,so researchers tried to reconstruct
his idea. The following is one of them.
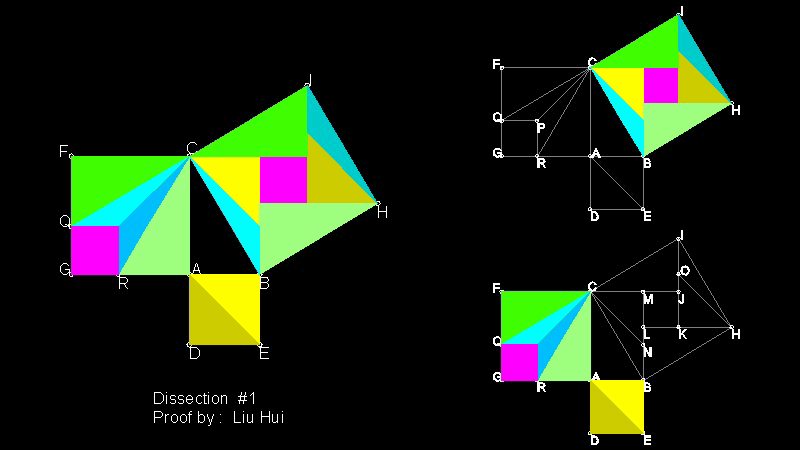
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type dissect_1
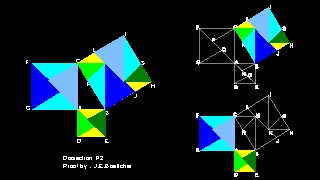
Proof by J.E.Böttcher using Dissection
Ref.1 lists the following dissection proof as Geometric Proofs #19 (p. 112) and
gives credit to Johannes Eduard Böttcher (1847 - 1919).
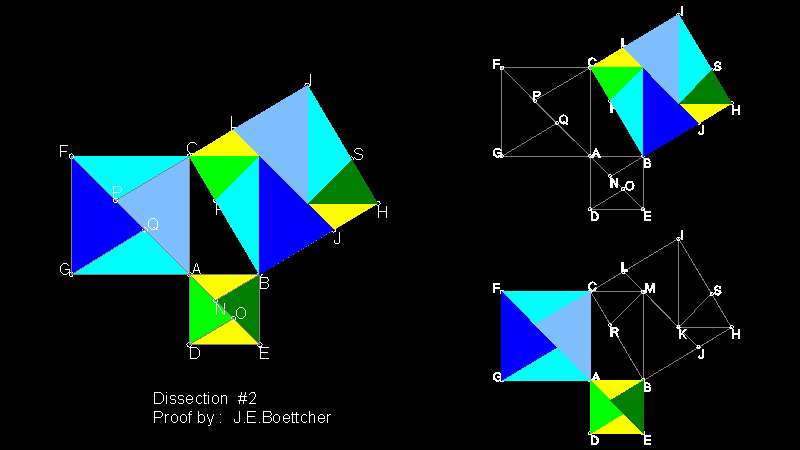
You can see the process in animation.
To create this drawing and animation:
Load Euclid_47.lsp (load "Euclid_47")
Then from command line, type dissect_2
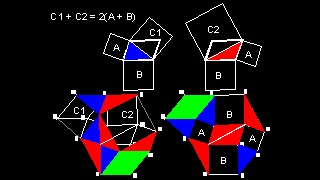
Generalized Pythagorean Theorem for a Parallelogram
This proof is published by David S. Wise (Ref. 9), and it was reprinted in Ref. 5 (p.9).
On Sept 14, 2011, the author ,David S. Wise, kindly notified me by e-mail as follows:
"I later found out that it was already known as Apollonius's parallelogram theorem."
When the parallelogram is a rectangle, this is Pythagorean theorem.
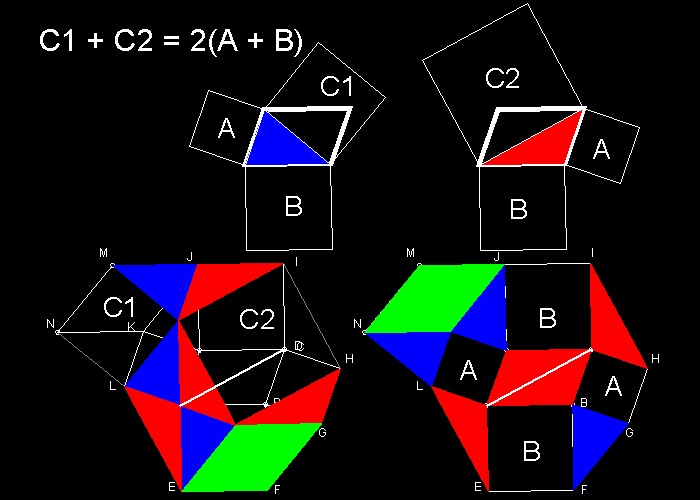
You can see the process in animation.
To create this drawing and animation:
Load gen_Pythagoras.lsp (load "gen_Pythagoras")
Then from command line, type gen_Pythagoras
De Gua's Theorem: Generalization of the Pythagorean theorem to three dimensions
De Gua's theorem is a generalization of the Pythagorean theorem to three dimensions and named for Jean Paul de Gua de Malves.(1712-1785)
This theorem was presented to the Paris Academy of Sciences in 1783.
If a tetrahedron has a right angle corner (a corner like a cube), then the square of the area of the face opposite the right angle corner
is the sum of the squares of the areas of the other three faces.
Then De Gua's theorem states
(Area of ABC)2= (area of OAB)2 + (area of OBC)2 + (area of OCA)2
Let OA = a, OB = b and OC = c.
Then this theorem can be written as follows:
(Area of ABC)2= (1/4){(ab)2 + (bc)2 + (ca)2}
One easy way to prove this is the use of Heron's formula for the area
of a triangle.
To create this drawing :
Load DeGua.lsp (load "DeGua")
Then from command line, type DeGua
Spherical Pythagorean Theorem
For a right triangle ABC on a sphere of radius R with a right angle at vertex C
and sides of length a,b,and c, then
cos(c/R) = cos(a/R) * cos(b/R) .
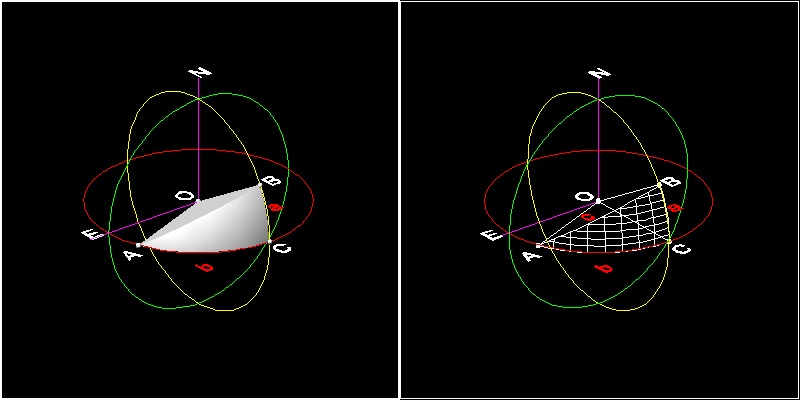
About this example model
red great circle represents equator, yellow one represents longitude line of zero and 180, and
green color represents longitude=90 degrees line.
Point A : 100 deg East and on the equator
Point B : 180 deg East and 30 deg North
Point C : 180 deg East and on the equator
Radius of the Earth is chosen to be 6373 km(=3956 mile).
To create this drawing :
Load haversine.lsp (load "haversine")
Then from command line, type sphere_pythagorean
SHADEMODE command is used to get Gouraud shading and 3D wireframe
Spherical Pythagoreantheorem states:
cos(c/R) = cos(a/R) * cos(b/R) (1)
Maclaurin series for cos(x) is :
cos(x) = 1 - x2/2! + x4/4! - x6/6! + ...
Using this formula in (1) gives us:
1 - (c/R)2/2 + (c/R)4/24 -...=
{1 - (a/R)2/2 + (a/R)4/24 -...}{1 - (b/R)2/2 + (b/R)4/24 -...}
=1 - (a/R)2/2 - (b/R)2/2 + (ab)2/(4 R4) +...
Or
c2 + (terms of higher powers of c)/R2
= a2 + b2 + (terms of higher powers of a & b)/R2
When R is large relative to a,b and c, then terms divided by R2 becomes negligibly small,
and we have a classical Pythagorean theorem ,i.e.
c2 = a2 + b2
Number check on this model
From the drawing shown above , it is possible to obtain arc length a,b and c.Keep exploding the 3D objects until it is not possible to explode anymore.
Then use LIST command to get arc length.
This is the result.
a = 3333.7534 b = 7778.7579 c = 8086.6416 and R = 6367
Use these values to compute cos(a/R),etc.
Just run the command check_theorem, and the results are
cos(a/R) = 0.866025
cos(b/R) = 0.34202
So cos(a/R)*cos(b/R) = 0.296198
This is very, very close the value of cos(c/R)
cos(c/R) = 0.296198
Finally*
cos(c/R)/{cos(a/R)*cos(b/R)} = 0.99999996
And for reference,
c2/{a2 + b2} = 0.91302773
*Note:This results are based on the number extracted from the graphical objects.
If all the length of a,b and c are computed using the trigonometry,
numerical precision is much higher (up to at least 12-th decimal place).
References
There are more books written about this subject than those listed here.
- Loomis,Elisha Scott: The Pythagorean Proposition, NCTM, 1968. Original published in 1927.
- Wells, David: The Penguin Disctionary of Curious and Interesting GEOMETRY. London,England: Penguin Books, p.198, 1991.(Out of print)
- Eves, Howard: The Great Moments in Mathematics Before 1650,Mathematical Association of America, 1983.
- Nelson,R.B. : Proofs Without Words: Exercises in Visual Thinking. MAA, 1993.
- Nelson,R.B. : Proofs Without Words II: More Exercises in Visual Thinking. MAA, 2000.
- Swetz,F.J.: From Five Fingers to Infinity,Open Court, 1996.
- Abe, Hisashi: "Amazing Origami"(in Japanese),2003. ISBN 4-535-78409-4
- Maor,Eli.: "The Pythagorean Theorem, A 4,000-year History",Princeton Univ.,2007.
- Wise,David S.: "Proof without words: Generalization from Pythagoras",Mathematics Magazine,vol. 71,no.1(Feb 1998),p.64
On Internet
- Pythagoras' Theorem, by Bill Casselman, The University of British Columbia.
- Many more interesting proofs by Alexander Bogomolny
- A proof of the Pythagorean Theorem by Liu Hui (third century AD)
reference for dissection Proof #9