Doubling the Cube
Go to   Fun_Math Content Table   Three Famous Problems   Origami Solutions

Origami(Paper Folding) Solution

Preparation--Haga's theorem - I (ref.1)

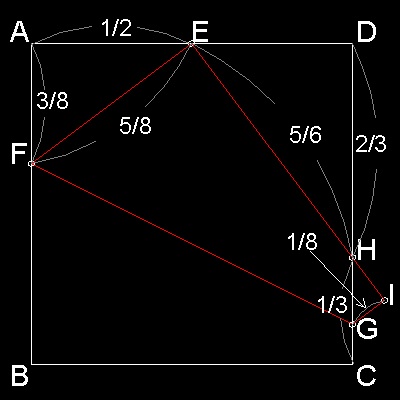
Place a square paper on the table. Mark a mid point E on the AD side.
Pick one corner of the paper (B) and move to the point E and slide your fingers pressing along the imaginary line connecting FG in the figure below.
Kazuo Haga (Ref.1) noticed that the result yields many interesting fractional numbers as shown in the figure.

Example case

Note that starting from a smallest denominator, fractional line segment lengths created are
1/3 , 2/3, 1/6, 5/6, 1/8, 3/8, 5/8.
It is interesting that we get fractions like 1/3 ,1/6 and 3/8 from 1/2.

This result was published in a Japanese mathematical journal in 1979 as "Haga's Theorem".
In ref.1 , Haga called this as "Haga's theorem 1", because there are 2 more developed since then. 
 
 Haga's theorem states:
	When one of the corner of the square paper
	is moved to fall onto the fractional point
	on other edge line,
	the folding process will create many fractional
	numbers.
In order to find these fractional numbers for cases other than 1/2, a simple computer program is required . The model is shown next:
******** Haga_theorem_1_sample.dwg ********

To create this drawing:
   Load Haga_number.lsp    (load "Haga_number")
  Then from command line, type Draw_Haga_1
The final step of displaying text must be done manually.
This will done automatically in the future update.

General case

 
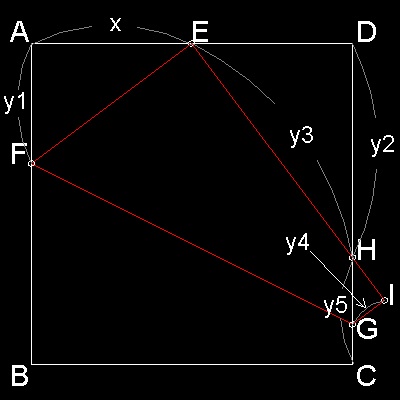
 Let AE = x, then
		y1 = (1 + x)(1 - x)/2 

		y2 = 2x /(1 + x)

		y3 = (1 + x2)/(1 + x)

		y4 = (1 - x)2/2

		y5 = 1 - y2

******** Haga_theorem_1_general.dwg ********

y1-y5 are shown in the figure below.

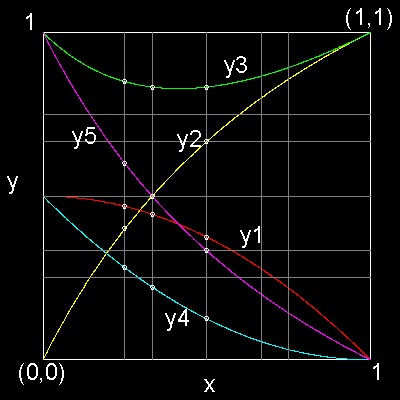
For x values of 1/2, 1/3 and 1/4,
actual points are shown by point marks.

It is interesting to note that the x_value which gives y1 = y2
is the solution of the equation :
x3 + x2 - 3x - 1 = 0

To create this drawing:
   Load Haga_number.lsp    (load "Haga_number")
  Then from command line, type Draw_Haga_number

Increment of x-value = 0.001
********** Haga_number_graph.dwg ********* 

 
  The result of computation up to denominator value 10 is shown below.
	*******	Haga's Number List *******

	 x      y1       y2       y3       y4      y5	
   -2-
	1/2      3/8     2/3       5/6      1/8    1/3
   -3-
	1/3      4/9     1/2       5/6      2/9    1/2
	2/3     5/18     4/5     13/15     1/18    1/5
   -4-
	1/4    15/32     2/5     17/20     9/32    3/5
	3/4     7/32     6/7     25/28     1/32    1/7
   -5-
	1/5    12/25     1/3     13/15     8/25    2/3
	2/5    21/50     4/7     29/35     9/50    3/7
	3/5     8/25     3/4     17/20     2/25    1/4
	4/5     9/50     8/9     41/45     1/50    1/9
   -6-
	1/6    35/72     2/7     37/42    25/72    5/7
	5/6    11/72   10/11     61/66     1/72   1/11
   -7-
	1/7    24/49     1/4     25/28    18/49    3/4
	2/7    45/98     4/9     53/63    25/98    5/9
	3/7    20/49     3/5     29/35     8/49    2/5
	4/7    33/98    8/11     65/77     9/98   3/11
	5/7    12/49     5/6     37/42     2/49    1/6
	6/7    13/98   12/13     85/91     1/98   1/13
   -8- 
	1/8   63/128     2/9     65/72   49/128    7/9
	3/8   55/128    6/11     73/88   25/128   5/11
	5/8   39/128   10/13    89/104    9/128   3/13
	7/8   15/128   14/15   113/120    1/128   1/15
   -9-
	1/9    40/81     1/5     41/45    32/81    4/5
	2/9   77/162    4/11     85/99   49/162   7/11
	4/9   65/162    8/13    97/117   25/162   5/13
	5/9    28/81     5/7     53/63     8/81    2/7
	7/9    16/81     7/8     65/72     2/81    1/8
	8/9   17/162   16/17   145/153    1/162   1/17
   -10-
	1/10  99/200    2/11   101/110   81/200   9/11
	3/10  91/200    6/13   109/130   49/200   7/13
	7/10  51/200   14/17   149/170    9/200   3/17
	9/10  19/200   18/19   181/190    1/200   1/19

To create this list:
   Load Haga_number.lsp    (load "Haga_number")
  Then from command line, type List_Haga_number
Then input the maximum denominator number (in this case 10).
The output file name is a text file named "Haga_number.txt".

In the next section, it becomes necessary to compute y1 value for x = 73/100
Case like this can be handled by executable haga_1 from the command line window.

Example input & ouput 

 
 Command: haga_1

 Denominator ?:100

 Numerator   ?:73
   Haga's Number List

  x         y1              y2             y3            y4          y5
 73/100 4671/20000       146/173     15329/17300       729/20000  27/173

2. Origami Solution by Kazuo Haga (ref.1)

Ref.1 shows how to make a side length (15329/20000) by folding a square paper.
You can see the process in animation.

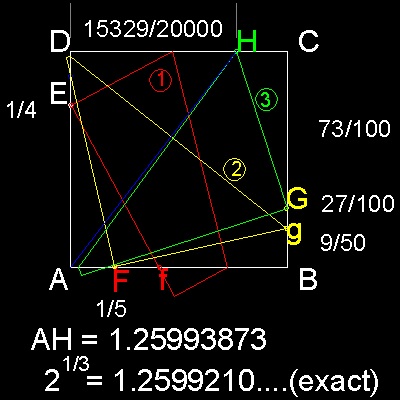
ABCD is a square paper.
Step 1: move side CB so that C matches point E.Side CD cuts line AB at point f. Find point F to bisect Af.
Step 2: move corner C to point F. Folding line cuts CB at point g. Extend Bg by 50 %, to define point G.
Step 3: move corner D to point G. Folding line cuts CD at point H.
Use the LIST command to obtain the properties of line AH. 
 
 from point, X=0.00000000  Y=0.00000000  Z=0.00000000
   to point, X=0.76645000  Y=1.00000000  Z=0.00000000
      Length =1.25993873,  Angle in XY Plane =     53
      Delta X =0.76645000, Delta Y = 1.0, Delta Z =0.0

AH3 = (1.25993873)3 = 2.0000841
So,length AH = 1.25993873 ,is a very good approximation of 21/3 = 1.259921...
********** Origami_Delian_2_desc.dwg *********

To create this drawing and animation:
   Load Haga_Delian.lsp    (load "Haga_Delian")
  Then from command line, type Haga_Delian

References

1. Haga, Kazuo: "Origamics part - I" , (in Japanese), 1999, ISBN 4-535-78293-8

Go to   Fun_Math Content Table   Three Famous Problems   Origami Solutions

All questions/suggestions should be sent to Takaya Iwamoto

Last Updated Jan 09, 2007

Copyright 2006 Takaya Iwamoto   All rights reserved .